Як визначити оптимальне рішення виробничого процесу. Яке рішення вважатимуться оптимальним? Графоаналітичний спосіб розв'язання задач лінійного програмування

Слід зазначити, що методи вирішення задач лінійного програмування відносяться. не до економіки, а до математики та обчислювальної техніки.При цьому економіст повинен забезпечити максимально комфортні умови діалогу з відповідним програмним забезпеченням. У свою чергу такі умови можуть забезпечувати лише динамічні та інтерактивні середовища розробки, що мають у своєму арсеналі набір необхідних для вирішення таких завдань бібліотек. Однією з середовищ розробки програмного забезпечення безумовно є Python.

Постановка задачі

У публікаціях розглядалися рішення прямих завдань оптимізації методом лінійного програмування та було запропоновано обгрунтований вибір решателя scipy. optimize.

Однак відомо, що кожній задачі лінійного програмування відповідає так звана виділена (двійна) завдання. У ній у порівнянні з прямим завданням рядки переходять у стовпці, нерівності змінюють знак, замість максимуму шукається мінімум (або навпаки, замість мінімуму - максимум). Завдання, подвійне до двоїстого - це саме вихідне завдання.

Вирішення двоїстої задачі дуже важливе для аналізу використання ресурсів. У даній публікації буде доведено, що оптимальні значення цільових функцій у вихідній та двоїстій задачі збігаються (тобто максимум у вихідному завданні збігається з мінімумом у двоїстій).

Оптимальні значення вартості матеріалу та праці оцінюватимуться за їх вкладом у цільову функцію. В результаті буде отримано «об'єктивно обумовлені оцінки» сировини та робочої сили, які не збігаються з ринковими цінами.

Вирішення прямої задачі про оптимальну виробничу програму

Враховуючи високий рівень математичної підготовки переважної більшості користувачів даного ресурсу не наводитиму балансові рівняння з верхніми та нижніми обмеженнями та введенням для переходу до рівностей додаткових змінних. Тому відразу наведу позначення змінних, що використовуються у рішенні:
N – кількість видів виробів;
m-кількість видів використовуваної сировини;
b_ub - вектор наявних ресурсів розмірності m;
A_ub – матриця розмірності m×N, кожен елемент якої є витратою ресурсу виду i виробництва одиниці виробу виду j;
з - вектор прибутку від виробництва одиниці виробу кожного виду;
x – шукані обсяги виробів кожного виду (оптимальний план виробництва) що забезпечують максимальний прибуток.

Функція мети
maxF(x)=c×x

Обмеження
A×x≤b

Чисельні значення змінних:
N=5; m=4; b_ub =; A_ub = [, , ,]; c =.

Завдання
1.Знайти x для забезпечення максимального прибутку
2. Знайти використані ресурси під час виконання п.1
3. Знайти залишки ресурсів (якщо вони є) під час виконання п.1

Для визначення максимуму (за замовчуванням визначається мінімум коефіцієнти цільової функції потрібно записати з негативним знаком c = [-25, -35, -25, -40, -30] та проігнорувати знак мінус перед прибутком.

Використання при виведенні результатів позначення:
x- Масив значень змінних, що доставляють мінімум (максимум) цільової функції;
slack- Значення додаткових змінних. Кожна змінна відповідає обмеженню-нерівності. Нульове значення змінної означає, що відповідне обмеження є активно;
success- True, якщо функції вдалося знайти оптимальне рішення;
status- Статус рішення:
0 - пошук оптимального рішення завершився успішно;
1 – досягнуто ліміт на кількість ітерацій;
2 – завдання немає рішень;
3 – цільова функція не обмежена.
nit– кількість зроблених ітерацій.

Лістинг розв'язання прямого завдання оптимізації

#!/usr/bin/python # -*- coding: utf-8 -*- import scipy from scipy.optimize import linprog # завантаження бібліотеки ЛП c = [-25, -35,-25,-40,-30] # список коефіцієнтів функції мети b_ub = # список обсягів ресурсів A_ub = [, # матриця питомих значень ресурсів , , ] d=linprog(c, A_ub, b_ub) # пошук рішення for key,val in d.items(): print(key ,val) # висновок рішення if key=="x": q=#використані ресурси print("A_ub*x",q) q1= scipy.array(b_ub)-scipy.array(q) #залишки ресурсів print(" b_ub-A_ub*x", q1)

Результати розв'язання задачі
nit 3
status 0

success True
x [ 0. 0. 18.18181818 22.72727273 150. ]
A_ub*x
b_ub-A_ub*x [ 0. 0. 0. 90.90909091]
fun -5863.63636364
slack [ 0. 0. 0. 90.90909091]

Висновки

1. Знайдено оптимальний план за видами продукції
2. Знайдено фактичне використання ресурсів
3. Знайдено залишок не використаного четвертого виду ресурсу [ 0. 0 0.0 0.0 90.909]
4. Немає потреби у обчисленнях за п.3, тому що той же результат виводити у змінній slack

Вирішення двоїстої задачі про оптимальну виробничу програму

Четвертий вид ресурсу у прямій задачі використана не повністю. Тоді цінність цього ресурсу для підприємства виявляється нижчою порівняно з ресурсами, що обмежують випуск продукції, і підприємство готове заплатити більшу ціну за придбання ресурсів, що дозволяють збільшити прибуток.

Введемо нове призначення шуканої змінної x як деякої «тіньової» ціни, що визначає цінність даного ресурсу щодо прибутку від реалізації продукції, що випускається.

C - Вектор наявних ресурсів;
b_ub - Вектор прибутку від виробництва одиниці виробу кожного виду;
A_ub_T - транспонована матриця A_ub.

Функція мети
minF(x)=c×x

Обмеження
A_ub_T ×x≥ b_ub

Чисельні значення та співвідношення для змінних:
з =; A_ub_T transpose(A_ub); b_ub =.

Завдання:
Знайти x показує цінність виробника кожного виду ресурсів.

Особливості рішення з бібліотекою scipy. optimize
Для заміни обмежень згори на обмеження з низу необхідно помножити на мінус одиницю обидві частини обмеження – A_ub_T ×x≥ b_ub… Для цього вихідні дані записати у вигляді: b_ub = [-25, -35,-25,-40,-30]; A_ub_T = - scipy.transpose(A_ub).

Лістинг розв'язання двоїстої задачі оптимізації

#!/usr/bin/python # -*- coding: utf-8 -*- import scipy from scipy.optimize import linprog A_ub = [, , , ] c= b_ub = [-25, -35,-25,- 40,-30] A_ub_T =-scipy.transpose(A_ub) d=linprog(c, A_ub_T, b_ub) для key,val in d.items(): print(key,val)

Результати розв'язання задачі
nit 7
Message Optimization виконано успішно.
fun 5863.63636364
x [2.27272727 1.81818182 6.36363636 0.]
slack [ 5.45454545 2.27272727 0. 0. 0. ]
status 0
success True

Висновки

Третій вид ресурсів має найбільшу цінність для виробника, тому даний вид ресурсів повинен бути закуплений в першу чергу, потім перший і другий вид. Четвертий вид ресурсу має для виробника нульову цінність та закуповується останнім.

Результати порівняння прямої та двоїстої задачі

1. Подвійне завдання розширює можливості планування випуску продукції, але засобами scipy. optimize вирішується за вдвічі більшу за пряму кількість ітерацій.
2. Змінна slack виводить інформацію про активність обмежень у вигляді нерівностей, які можуть бути використані, наприклад, для аналізу залишків сировини.
3. Пряме завдання є завданням максимізації, а подвійне - завданням мінімізації, і навпаки.
4. p align="justify"> Коефіцієнти функції мети в прямій задачі є обмеженнями в двоїстій задачі.
5. Обмеження у прямій задачі стають коефіцієнтами функції мети у подвійній.
6. Знаки нерівностей в обмеженнях змінюються протилежними.
7. Матриця системи рівностей транспонується.

ПосиланняОптимізація лінійних моделей у MS Excel проводиться симплекс-методом- цілеспрямованим перебором опорних розв'язків задачі лінійного програмування. Алгоритм симплекс-метода зводиться до побудови опуклого багатогранника в багатовимірному просторі, а потім перебору його вершин з метою пошуку екстремального значення цільової функції.

Ефективні засоби лінійного програмуваннялежать в основі цілісного і нелінійного програмування для вирішення складніших завдань оптимізації. Ці методи, однак, потребують більш тривалого часу для обчислень.

У наступних лекціях будуть детально розібрані приклади вирішення типових задач оптимізації та прийняття управлінських рішень за допомогою надбудови MS Excel "Пошук рішення". Завдання, які найкраще вирішуються цим засобом, мають три основні властивості:

• є єдина мета, функціонально пов'язана з іншими параметрами системи, яку потрібно оптимізувати (знайти її максимум, мінімум чи певне числове значення);
• є обмеження, що виражаються, як правило, у вигляді нерівностей (наприклад, обсяг сировини, що використовується, не може перевищувати запасів сировини на складі, або час роботи верстата за добу не повинен бути більше 24 годин мінус час на обслуговування);
• є набір вхідних значень-змінних, що впливають на величини, що оптимізуються, і на обмеження.

Параметри завдань обмежуються такими граничними показниками:

• кількість невідомих – 200;
• кількість формульних обмежень на невідомі – 100;
• кількість граничних умов на невідомі – 400.

Алгоритм пошуку оптимальних рішень включає кілька етапів:

• підготовчі роботи;
• налагодження рішення;
• аналіз рішення.

Послідовність необхідних підготовчих робіт, що виконуються під час вирішення завдань економіко-математичного моделювання за допомогою MS Excel, наведена на блок-схемі малюнка 1.6.

Мал. 1.6.

Із наведених п'яти пунктів плану підготовчих робіт лише п'ятий пункт формалізується. Інші роботи вимагають творчості - і різними людьми вони можуть бути виконані по-різному. Коротко пояснимо суть формулювань пунктів плану.

При постановці завдання відомі цільові коефіцієнти та нормовані коефіцієнти. У попередньому прикладі коефіцієнтами, що формують цільову функцію, були значення нормованого прибутку на одну полицю типу ( ) та одну полицю типу ( ). Нормованими коефіцієнтами служили норми витрати матеріалу та машинного часу на одну полицю кожного типу. Матриця мала такий вигляд:

Крім того, завжди відомі значення ресурсів. У попередньому прикладі це був тижневий запас дощок та можливості використовувати машинний час: , . Часто у завданнях значення змінних потрібно обмежити. Тому потрібно визначити нижню та верхню межі області їх змін.

Таким чином, у діалоговому вікні оптимізаційної програми "Пошук рішення" ми повинні задати наступний цільовий алгоритм:

Цільова функція дорівнює добутку вектора значень значень змінних на вектор цільових коефіцієнтів

Нормованих коефіцієнтів на вектор змінних значень не повинен перевищувати значення заданого вектора ресурсів

Значення змінної повинні знаходитись у заданих межах число вихідних елементів системи

Число вихідних елементів системи

Число заданих видів ресурсів

Налагодження рішення необхідне у разі, коли програма видає повідомлення про негативні результати (рисунок 1.7):

Мал. 1.7.

• якщо не отримано припустиме рішення, виконати коригування моделі вихідних даних;
• якщо не отримано оптимальне вирішення, то ввести додаткові обмеження.

Програма видає оптимальне вирішеннятільки для моделі реальної проблеми, а не вирішення самої проблеми. При побудові моделі були зроблені різні полегшення припущення реальної ситуації. Це дозволило формалізувати процес, наближено відобразивши реальні кількісні залежності між параметрами системи та метою. А якщо реальні параметри відрізнятимуться від тих, що закладені в моделі, то як зміниться рішення? Щоб дізнатися про це, перед прийняттям управлінського рішення проводять аналіз рішення моделі.

Аналіз оптимального рішення, вбудований у програму, є заключним етапом математичного моделювання економічних процесів. Він дозволяє здійснити глибшу перевірку відповідності моделі процесу, а також надійність оптимального рішення. Він ґрунтується на даних оптимального рішеннята звітів, що видаються у "Пошуку рішення". Але він не виключає та не замінює традиційного аналізу плану з економічних позицій перед прийняттям управлінського рішення.

Економічний аналіз ставить перед собою такі цілі:

• визначення можливих наслідків у системі загалом та її елементах при зміні параметра моделі;
• оцінка стійкості оптимального плану до зміни окремих параметрів завдання: якщо він не стійкий до зміни більшості параметрів, знижується гарантія виконання та досягнення розрахованого оптимуму;
• проведення варіантних розрахунків та отримання нових варіантів плану без повторного вирішення завдання від вихідного базису за допомогою коригування.

Можливі методи аналізу представлені у схемі малюнку 1.8 .

Після отримання оптимального рішення проводиться його аналіз щодо отриманих звітів. Аналіз стійкості- Вивчення впливу змін окремо взятих параметрів моделі на показники оптимального рішення. Аналіз меж- аналіз допустимих змін у оптимальному плані, у якому план залишається оптимальним.

Враховуючи відповідальність ухвалення економічного управлінського рішення, Керівник повинен переконатися, що отриманий оптимальний план є єдино вірним. Для цього треба на основі моделі отримати відповіді на такі запитання:

• "що буде якщо…"
• "що треба, щоб…"

Аналіз з метою відповіді на перше запитання називається варіантним аналізом; аналіз з метою відповіді на друге питання називається рішеннями на замовлення.

Варіантний аналіз буває наступних видів:

• Параметричний- аналіз, який полягає у вирішенні задачі за різних значень деякого параметра.
• Структурний аналіз- коли розв'язання задачі оптимізації шукається за різної структури обмежень.
• Багатокритеріальний аналіз- це вирішення задачі з різних цільових функцій.
• Аналіз за умовних вихідних даних- коли вихідні дані, використовувані під час вирішення завдання, залежить від дотримання додаткових умов.

Після проведення аналізу слід подати результати у графічній формі та скласти звіт із рекомендаціями про прийняття рішення з урахуванням конкретної економічної ситуації.

Універсальний метод розв'язання задач ЛП називається симплекс-методом. Застосування цього і його найчастіше зустрічається модифікації - двухфазного симплекс-метода.

При графічному способі розв'язання завдань ЛП ми фактично з безлічі вершин, що належать межі безлічі рішень системи нерівностей, вибрали таку вершину, в якій значення цільової функції досягало максимуму (мінімуму). У разі змінних цей метод цілком наочний і дозволяє швидко знаходити рішення задачі.

Якщо задачі три і більше змінних, а реальних економічних завданнях саме така ситуація, важко уявити наочно область рішень системи обмежень. Такі завдання вирішуються за допомогою симплекс-метода чи методом послідовних поліпшень. Ідея методу проста і полягає у наступному.

За певним правилом знаходиться первісний опорний план (деяка вершина області обмежень). Перевіряється, чи є план оптимальним. Якщо так, то завдання вирішено. Якщо ні, то переходимо до іншого покращеного плану – до іншої вершини. значення цільової функції у цьому плані (у цій вершині) явно краще, ніж у попередньої. Алгоритм переходу здійснюється за допомогою деякого обчислювального кроку, який зручно записувати у вигляді таблиць симплекс-таблицями . Так як вершин кінцеве число, то за кінцеве число кроків ми приходимо до раціонального рішення.

Розглянемо симплексний метод конкретному прикладі завдання упорядкування плану.

Ще раз зауважимо, що симплекс-метод застосуємо для вирішення канонічних завдань ЛП, наведених до спеціального вигляду, тобто мають базис, позитивні праві частини та цільову функцію, виражену через небазисні змінні. Якщо завдання не приведено до спеціального вигляду, то потрібні додаткові кроки, про які ми поговоримо пізніше.

Розглянемо завдання план виробництва, попередньо побудувавши модель і привівши її до спеціального виду.

Завдання.

Для виготовлення виробів Аі Усклад може відпустити сировини трохи більше 80 одиниць. Причому виготовлення виробу Авитрачається дві одиниці, а вироби У- Одна одиниця сировини. Потрібно спланувати виробництво так, щоб був забезпечений найбільший прибуток, якщо виробів Апотрібно виготовити не більше 50 шт., а виробів У- Не більше 40 шт. Причому прибуток від реалізації одного виробу А- 5 руб., а від У- 3 руб.

Побудуємо математичну модель, позначивши за х 1 кількість виробів А в плані, х 2 - кількість виробів У. тоді система обмежень буде виглядати так:

x 1 ≤50
x 2 ≤40
2x 1 +x 2 ≤80
x 1 ≥0, x 2 ≥0
5x 1 +3x 2 →max

Наведемо завдання до канонічного вигляду, ввівши додаткові змінні:

x 1 +x 3 =50
x 2 +x 4 =40
2x 1 +x 2 +x 5 =80
x 1 ≥0, x 2 ≥0
5x 1 +3x 2 →max
-F = -5x1 - 3x2 → min.

Це завдання має спеціальний вид (з базисом, праві частини невід'ємні). Її можна вирішити симплекс-методом.

Iетап.Запис завдання до симплекс-таблиці. Між системою обмежень задачі (3.10) та симплекс-таблицею взаємно-однозначна відповідність. Рядків у таблиці стільки, скільки рівностей у системі обмежень, а стовпців - стільки, скільки вільних змінних. Базові змінні заповнюють перший стовпець, вільні - верхній рядок таблиці. Нижній рядок називається індексним, у ньому записуються коефіцієнти при змінних у цільовій функції. У правому нижньому куті спочатку записується 0, якщо функції немає вільного члена; якщо є, то записуємо його із протилежним знаком. На цьому місці (у правому нижньому кутку) буде значення цільової функції, яке при переході від однієї таблиці до іншої повинне збільшуватися по модулю. Отже, нашій системі обмежень відповідає таблиця 3.4 і можна переходити до II етапу рішення.

Таблиця 3.4

базисні			вільні

IIетап. Перевірка опорного плану оптимальність.

Ця таблиця 3.4 відповідає наступний опорний план:

(х 1 , х 2 , х 3 , х 4 , х 5) = (0, 0, 50, 40, 80).

Вільні змінні х 1 , х 2 дорівнюють 0; х 1 = 0, х 2 = 0. А базисні змінні х 3 , х 4 , х 5 приймають значення х 3 = 50, х 4 = 40, х 5 = 80 – зі стовпця вільних членів. Значення цільової функції:

-F = - 5х 1 - 3х 2 = -5 · 0 - 3 · 0 = 0.

Наше завдання – перевірити, чи є даний опорний план оптимальним. для цього необхідно переглянути індексний рядок - рядок цільової функції F.

Можливі різні ситуації.

1. В індексній F-Рядок немає негативних елементів. Отже, план оптимальний, можна виписати розв'язання задачі. Цільова функція досягла свого оптимального значення, що дорівнює числу, що стоїть у правому нижньому кутку, взятому з протилежним знаком. Переходимо до IV етапу.

2. В індексному рядку є хоча б один негативний елемент, у стовпці якого немає позитивних. Тоді робимо висновок у тому, що цільова функція F→∞ необмежено зменшується.

3. В індексному рядку є негативний елемент, у стовпці якого є хоча б один позитивний. Тоді переходимо до наступного ІІІ етапу. перераховуємо таблицю, покращуючи опорний план.

IIIетап. Поліпшення опорного плану.

З негативних елементів індексної F-Рядки виберемо найбільший по модулю, назвемо відповідний йому стовпець роздільним і позначимо "".

Щоб вибрати роздільну здатність, необхідно обчислити відносини елементів стовпця вільних членів тількидо позитивнимелементам роздільного стовпця. Вибрати із отриманих відносин мінімальне. Відповідний елемент, на якому досягається мінімум, називається роздільною здатністю. Виділятимемо його квадратом.

У прикладі, елемент 2 - вирішальний. Рядок, що відповідає цьому елементу, теж називається роздільною (табл. 3.5).

Таблиця 3.5

Вибравши роздільну здатність, робимо перелік таблиці за правилами:

1. У новій таблиці таких самих розмірів, як і раніше, змінні роздільної здатності і стовпця змінюються місцями, що відповідає переходу до нового базису. У нашому прикладі: х 1 входить у базис, замість х 5, яка виходить із базису і тепер вільна (табл. 3.6).

Таблиця 3.6

2. На місці роздільної здатності елемента 2 записуємо зворотне йому число ½.

3. Елементи роздільної здатності ділимо на роздільний елемент.

4. Елементи роздільного стовпця ділимо на роздільну здатність і записуємо з протилежним знаком.

5. Щоб заповнити елементи таблиці 3.6, що залишилися, здійснюємо перерахунок за правилом прямокутника. Нехай ми хочемо порахувати елемент на місці 50.

З'єднуємо цей елемент подумки з вирішальним, знаходимо твір, віднімаємо твір елементів, що знаходяться на іншій діагоналі прямокутника, що вийшов. Різницю ділимо на роздільний елемент.

Отже, . Записуємо 10 на місце, де було 50. Аналогічно:
, , , .

Таблиця 3.7

Маємо нову таблицю 3.7, базисними змінними тепер є змінні (x3, x4, x1). Значення цільової функції дорівнювало -200, тобто. поменшало. Щоб перевірити це базове рішення на оптимальність треба перейти знову до II етапу. Процес, очевидно, кінець, критерієм зупинки є пункт 1 і 2 II етапу.

Доведемо розв'язання задачі до кінця. Для цього перевіримо індексний рядок і, побачивши в ньому негативний елемент -½, назвемо відповідний йому стовпець роздільною здатністю і, згідно з III етапом, перерахуємо таблицю. Склавши відносини і вибравши серед них мінімальне = 40, визначили роздільну здатність елемент 1. Тепер перерахунок здійснюємо згідно з правилами 2-5.

Таблиця 3.8

Після перерахунку таблиці переконуємося, що у індексному рядку немає негативних елементів, отже, завдання вирішено, базисний план є оптимальним.

IVетап. Виписування раціонального рішення.

Якщо симплекс-метод зупинився згідно з пунктом 1 II етапу, рішення завдання виписується наступним чином. Базисні змінні набувають значення стовпця вільних членів відповідно. У нашому прикладі х 3 = 30, х 2 = 40, х 1 = 20. Вільні змінні дорівнюють 0, х 5 = 0, х 4 = 0. Цільова функція набуває значення останнього елемента стовпця вільних членів із протилежним знаком: - F = -220 → F= 220, у прикладі функція досліджувалася на min, і спочатку F→ max, тому фактично символ змінився двічі. Отже, х* = (20, 40, 30, 0, 0), F* = 220. Відповідь до завдання:

Необхідно до плану випуску включити 20 виробів типу А, 40 виробів типу В, при цьому прибуток буде максимальним і дорівнюватиме 220 руб.

Наприкінці цього параграфа наведемо блок-схему алгоритму симплекс-метода, яка в точності повторює етапи, але, можливо, для деяких читачів буде зручніша у користуванні, тому що стрілочки вказують чітку спрямованість дій.

Посилання над прямокутниками у блок-схемі показують, якого етапу чи підпункту належить відповідна група перетворень. правило знаходження початкового опорного плану буде сформульовано у пункті 3.7.

Приклад. Вирішити наступне завдання ЛП у канонічній формі симплекс-методом.
f(x)=x 1 +9x 2 +5x 3 +3x 4 +4x 5 +14x 6 → min
x 1 +x 4 =20
x 2 +x 5 =50
x 3 +x 6 =30
x 4 +x 5 +x 6 =60
x i ≥ 0, i = 1,…,6
Говорять, що завдання ЛП має канонічну форму, якщо всі обмеження (крім умов невід'ємності змінних) мають вигляд рівностей, а всі вільні члени невід'ємні. Отже, ми маємо завдання в канонічній формі.
Ідея симплекс-методу полягає у наступному. Спочатку потрібно визначити деяку (початкову) вершину багатогранника допустимих рішень (початкове допустиме базисне рішення). Потім слід перевірити це рішення на оптимальність. Якщо вона оптимальна, то рішення знайдено; якщо ні, то перейти до іншої вершини багатогранника і знову перевірити оптимальність. Через кінцівки вершин багатогранника (наслідок кінцівки обмежень завдання ЛП) за кінцеве число "кроків" ми знайдемо точку мінімуму або максимуму. Слід зазначити, що з переході від однієї вершини до інший значення цільової функції зменшується (у задачі мінімум) чи зростає (у задачі максимум).
Таким чином, ідея симплекс-методу ґрунтується на трьох властивостях задачі ЛП.
Рішення.Щоб визначити початкове допустиме базисне рішення, тобто. щоб визначити базисні змінні, систему (5.6) потрібно призвести до "діагонального" вигляду. Застосовуючи метод Гауса (метод послідовного виключення невідомих), отримуємо з (5.6):
x 2 +x 1 +x 3 =40
x 4 +x 1 =20
x 5 -x 1 -x 3 = 10
x 6 +x 3 =30
Отже, базисними є змінні x 2 x 4 x 5 x 6їм надаємо значення, рівні вільним членам відповідних рядків: x 2 = 40, x 4 = 20, x 5 = 10, x 6 = 30,. Змінні x 1і x 3є небазисними: x 1 = 0, x 3 = 0.
Побудуємо початкове допустиме базисне рішення
x 0 = (0,40,0,20,10,30) (5.9)
Для перевірки оптимальності знайденого рішення x 0Необхідно з цільової функції виключити базові змінні (за допомогою системи (5.8)) і побудувати спеціальну симплекс таблицю.
Після виключення змінних цільову функцію зручно записати у вигляді:
f(x) = -7x 1 - 14x 3 +880 (5.10)
Тепер за допомогою (5.8) - (5.10) складаємо початкову симплекс-таблицю:

У нульовий рядок записані коефіцієнти зі зворотним знаком відповідних змінних при цільовій функції. Критерій оптимальності (для завдання на пошук мінімуму): допустиме базисне рішення ( x 0) оптимально, якщо в нульовому рядку немає жодного строго позитивного числа (крім значення цільової функції (880)). Це поширюється і такі ітерації (таблиці). Елементи нульового рядка називатимемо оцінками стовпців.
Отже, початкове допустиме базисне рішення (5.9) неоптимально: 7>0, 14>0 .
У нульовому стовпчику записані значення базових змінних. Вони обов'язково мають бути невід'ємними (див. рівняння (5.7)). Від першого до четвертого рядка написані коефіцієнти змінних із системи (5.8).
Так як x 0неоптимально, треба перейти до іншої вершині багатогранника допустимих рішень (побудувати нове д.б.р.). Для цього потрібно знайти провідний елемент та провести певне перетворення (симплексне перетворення).
Спочатку знаходимо провідний елемент таблиці, який стоїть у перетині провідного стовпчика (стовпець з найбільшою позитивною оцінкою) та провідного рядка (рядки, що відповідає мінімальному співвідношенню елементів нульового стовпчика до відповідних елементів (строго позитивних) провідного стовпчика).
У таблиці 1 провідний стовпчик - третій стовпчик, і провідний рядок - четвертий рядок (min(40/1,30/1)=30/1)позначені стрілками, а провідний елемент – кружечком. Провідний елемент показує, що базову змінну x 6потрібно замінити на небазову x 3. Тоді новими базовими змінними будуть x 2 , x 3 , x 4 , x 5, а небазисними - x 1 , x 6 ,. Це означає перехід до нової вершині багатогранника допустимих рішень. Щоб знайти значення координат нового допустимого базового рішення x 00потрібно будувати нову симплекс-таблицю і провести у ній елементарні перетворення:
а)всі елементи провідного рядка поділити на провідний елемент, перетворивши цим провідний елемент в 1 (для простоти викладок);
б)за допомогою провідного елемента (рівного 1) всі елементи провідного стовпчика перетворити на нулі (аналогічно методу виключення невідомих);
В результаті в нульовому стовпці отримано значення нових базисних змінних x 2 , x 3 , x 4 , x 5(див. таблицю 2) – базисні компоненти нової вершини x 00(Небазисні компоненти x 1 = 0, x 6 = 0,).

Як показує таблиця 2, нове базисне рішення x 00 = (0,10,30,20,40,0)неоптимально (у нульовому рядку є невід'ємна оцінка 7). Тому із провідним елементом 1 (див. таблицю 2) будуємо нову симплекс-таблицу, тобто. будуємо нове допустиме базисне рішення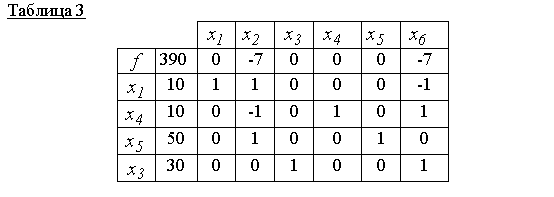

Таблиці 3 відповідає припустиме базисне рішення x 000 = (10,0,30,10,50,0)і його оптимально, т.к. в нульовому рядку немає позитивних оцінок. Тому f(x 000)=390є мінімальне значення цільової функції.
Відповідь: x 000 = (10, 0, 30, 10, 50, 0)- точка мінімуму, f(x 000)=390.

Умовно стандартне завдання лінійного програмування

Необхідно виконати у зазначеному порядку такі завдання.

1. Знайти оптимальний план прямого завдання:
   а) графічним методом;
   б) симплекс-метод (для побудови вихідного опорного плану рекомендується використовувати метод штучного базису).
2. Побудувати подвійне завдання.
3. Знайти оптимальний план двоїстої задачі з графічного рішення прямої, використовуючи умови, що доповнює нежорсткості.
4. Знайти оптимальний план двоїстої задачі по першій теоремі двоїстості, використовуючи остаточну симплекс-таблицю, отриману при вирішенні прямої задачі (див. п. 1б). Перевірити твердження «значення цільових функцій пари двоїстих завдань на своїх оптимальних рішеннях збігаються».
5. Подвійну задачу вирішити симплекс-методом, потім, використовуючи остаточну симплекс-таблицю двоїстої задачі знайти оптимальний план прямої задачі за першою теоремою двоїстості. Порівняти результат із результатом, отриманим графічним методом (див. п. 1а).
6. Знайти оптимальне ціле рішення:
   а) графічним методом;
   б) Методом Гоморі.
   Порівняти значення функцій цілочисленного та нецілочисленного рішень

Запитання для самоконтролю

1. Як будується симплекс-таблиця?
2. Як відображається зміна базису таблиці?
3. Сформулюйте критерій зупинки симплекс-метода.
4. Як організувати перерахунок таблиці?
5. З якого рядка зручно розпочинати перерахунок таблиці?

Якщо в щойно розглянутій задачі перше отримане базисне рішення виявилося допустимим, то в інших випадках його можна знайти не відразу, а через кілька кроків.

При цьому треба пам'ятати, що на першому етапі симплексного методу, тобто при знаходженні будь-якого допустимого рішення, лінійна форма до уваги не береться, а всі перетворення відносяться тільки до системи обмежень.

Нехай завдання лінійного програмування поставлено у загальному вигляді, тобто. системою m лінійних рівнянь із n змінними (m

Отже, цьому способу розбиття змінних на основні та неосновні відповідає базисне рішення …; 0; 0; ...; 0.

Розглянемо загальний випадок, коли це рішення є неприпустимим. Від отриманого базисного рішення слід спочатку перейти до якогось припустимого базисного рішення, причому не обов'язково, щоб цей перехід здійснювався відразу, в один крок.

Якщо система обмежень не суперечлива, через кінцеве число кроків буде здійснено перехід до допустимому базисному решению.

За припущенням, вихідне базисне рішення є неприпустимим. Отже, серед вільних членів системи обмежень є хоча б один негативний (кількість негативних вільних членів цієї системи збігається з числом негативних компонент вихідного базисного рішення). Нехай ним є вільний член k i i-ro рівняння, тобто основна змінна x iу відповідному базисному рішенні негативна.

Для переходу до нового базисного рішення необхідно вирішити два питання:

1) встановити, яка неосновна змінна повинна бути переведена до основних;

2) вибрати змінну, яку з основних слід перевести в неосновні на місце, що вибула в основні змінної.

При переведенні неосновної змінної в основні вона не зменшується, а, як правило, зростає: замість нуля у вихідному базисному рішенні вона набуде позитивного значення в новому базисному рішенні (виняток має місце тільки при виродженні). Тому для вирішення питання про те, які неосновні змінні можна перевести в основні, потрібно вміти знаходити неосновні змінні, зі збільшенням яких зростає основна змінна, негативна у вихідному базисному рішенні. Повернемося до i-го рівняння системи, в якому вільний член k iвід'ємний. Воно показує, що змінна x iзростає у разі зростання тих неосновних змінних, коефіцієнти яких у цьому рівнянні позитивні. Звідси випливає, що у основні можна перекладати ті неосновні змінні, які у рівнянні системи з негативним вільним членом мають позитивні коефіцієнти.

Тут можуть трапитися три випадки.

1. У i-му рівнянні системи немає неосновних змінних з позитивними коефіцієнтами, тобто всі коефіцієнти b i , jнегативні (як і вільний член k i).І тут дана система обмежень несовместна – вона має жодного допустимого рішення. Дійсно, внаслідок невід'ємності всіх змінних, у тому числі x m + l, ..., x n, i-го рівняння, в якому вільний член k iі всі коефіцієнти b i , m + l ,...,b i , nнегативні, випливає, що змінна x i- не може набувати невід'ємних значень. Але якщо немає жодного допустимого рішення системи обмежень, то немає оптимального.

2. У i-му рівнянні є одна змінна х т+j,коефіцієнтпри якій позитивний. І тут саме ця змінна перетворюється на основні.

3. У i-му рівнянні є кілька змінних із позитивними коефіцієнтами. В цьому випадку в основні можна перекласти будь-яку з них.

Далі необхідно встановити, яка основна змінна має бути переведена до числа неосновних. Для цього слід скористатися правилом: знаходять відношення вільних членів до коефіцієнтів при змінній, що переводиться в основні, з усіх рівнянь, де знаки вільних членів та зазначених коефіцієнтів протилежні, а потім розглядають абсолютну величину цих відносин і з них обирають найменшу (якщо в деяких рівняннях знаки вільних членів та коефіцієнтів збігаються або в якихось рівняннях змінна, що переводиться в основні, відсутня, то відношення вважають рівним ∞).

Рівняння, з якого одержано найменше відношення, виділяють. Виділене рівняння показує, яка з основних змінних має бути переведена в неосновні. Висловивши нові основні змінні через неосновні, переходять до наступного базисного рішення.

У результаті виходить аналогічна системі система рівнянь, у якій кількість негативних вільних кленів або збігається зі своїм числом у системі, або одиницю менше. Це залежить від того, позитивний або від'ємний вільний член у виділеному рівнянні.

Якщо виділеному рівнянні вільний член негативний, то новому базисному рішенні кількість негативних компонент виявиться на одиницю менше, ніж у вихідному. Якщо ж у виділеному рівнянні вільний член позитивний (або дорівнює нулю), то в новому базисному рішенні кількість негативних компонентів залишиться таким же, як і у вихідному.

Отже, виходить нове, покращене базисне рішення, яке ближче до області допустимих рішень системи обмежень. Якщо воно виявиться неприпустимим, то до нього слід застосувати ту саму схему ще раз. В результаті через кінцеве число кроків вийде допустиме базове рішення.

Продовження прикладу 4.1.Потрібно знайти таке допустиме базисне рішення цієї системи обмежень, яке б максимізувало лінійну форму.

Оскільки система обмежень є система чотирьох незалежних рівнянь із шістьма змінними, число основних змінних має дорівнювати чотирма, а число неосновних - двом.

Для вирішення задачі симплексним методом, перш за все, потрібно знайти будь-яке базове рішення. У цьому випадку це легко зробити. Для цього достатньо взяти як основні додаткові змінні. х 3 , х 4 , х 5 , х 6 . Так як коефіцієнти при цих змінних утворюють одиничну матрицю, відпадає необхідність обчислювати визначник. Вважаючи неосновні змінні х 1 , x 2 рівними нулю, отримаємо базисне рішення (0; 0; 120; 160; 120; 80), яке до того ж виявилося допустимим. Тому тут відпадає необхідність застосування першого етапу симплексного способу.

Переходимо відразу другого етапу, т. е. до пошуків оптимального рішення.

1 крок. Основні змінні: х 3, х 4, х 5, х 6; неосновні змінні: х 1 , x 2 . У системі основні змінні виразимо через неосновні. Для того щоб судити, чи залишити неосновні змінні в числі неосновних або їх вигідніше з точки зору наближення до оптимального рішення перевести в основні, слід виразити через них і лінійну форму (у даному випадку вона вже виражена через змінні х 1 , x 2) Тоді отримаємо:

При х 1 = х 2 = 0 маємо х 3 = 120, х 4 = 160, х 5 = 120, х 6 = 80, що дає базисне рішення (0; 0; 120; 160; 120; 80), яке ми прийняли за вихідне. У цьому базисному рішенні значення лінійної форми =0.

Коли ми думали х 1 = х 2 = 0 (виробництво нічого не випускає), була поставлена ​​мета - знайти перше, байдуже яке, базисне рішення. Цю мету досягнуто. Тепер від цього первісного рішення потрібно перейти до іншого, у якому значення лінійної форми збільшиться. З розгляду лінійної форми видно, що її значення зростає зі збільшенням значень змінних х 1 та х 2 . Іншими словами, ці змінні невигідно вважати неосновними, тобто рівними нулю, їх потрібно перевести до основних. Це означає перехід до нового базисному решению. При симплексному методі кожному кроці рішення передбачається переведення до основних лише однієї з вільних змінних. Переведемо до основних змінну х 2 оскільки вона входить у вираз лінійної форми з великим коефіцієнтом.

Як тільки одна з вільних змінних переходить до основних, одна з основних повинна бути переведена на її місце в число неосновних. Яку ж із чотирьох основних змінних потрібно вивести? Відповісти це питання допоможуть такі міркування.

Значення х 2 необхідно зробити якомога більшим, так як це відповідає кінцевій співі - максимізації F. Однак виявляється, що збільшення х 2 може продовжуватися лише до відомих кордонів, а саме доти, доки не порушиться вимога невід'ємності змінних. Так, з першого рівняння системи випливає, що змінна х 2 має перевищувати числа 120/4, тобто. х 2 ≤30, оскільки лише за цих значень х 2 змінна х 3 залишається позитивною (якщо х 2 = 30, то х 3 = 0; якщо ж х 2> 30, то х 3 < 0). Из третьего уравнения системы следует, что х 2 ≤ 120/2, тобто. х 2 ≤ 60, з четвертого - що х 2 ≤ 80/2, тобто. х 2 ≤ 40 (у другому рівнянні змінна х 2 не входить). Всім цим умовам задовольняє х 2 ≤ 30.

Іншими словами, для відповіді на питання, яку змінну потрібно перевести до числа неосновних, потрібно прийняти х 2 = min (120/4; 120/2; 80/2) = min (30; 60; 40) = 30. Тоді х 3 = 0 і х 3 переходить до числа неосновних змінних, а х 4 і х 5 залишаться позитивними,

2 крок. Основні змінні: х 2 , х 4 , х 5 , х 6 неосновні змінні: х 1 та х 3 . Виразимо основні змінні та лінійну форму через неосновні. У системі беремо те рівняння, з якого отримано мінімальне значення відношення вільного члена до коефіцієнта при х 2 . У разі це перше рівняння. Виразивши з цього рівняння х 2 , маємо, х 2 = 30 - 0.25 · х 3 . Підставимо цей вираз х 2 у всі інші рівняння системи (4.4) та в лінійну форму Fі, навівши подібні члени, отримаємо

При х 1 = х 3 = 0 маємо F = 90. Це вже краще, ніж на 1 кроці, але не потрібний максимум. Подальше збільшення функції Fможливе за рахунок введення змінної х 1 до основних; оскільки ця змінна входить у вираз Fз позитивним коефіцієнтом, тому його збільшення призводить до збільшення лінійної форми та її невигідно вважати неосновною, тобто. рівною нулю.

Для відповіді на питання, яку змінну вивести з основних до неосновних, приймемо х 1 = min (160/4; 60/2; 20/1) = 20. Тоді х 6 = 0 і х 6 переходить до числа неосновних змінних, а х 4 та х 5 залишаються при цьому позитивними.

Перше рівняння не використовується при знаходженні зазначеного мінімуму, оскільки х] не входить до цього рівняння.

3 крок. Основні змінні: х 1 , х 2 , х 4 ,х 5; неосновні змінні: х3, х6. Виразимо основні змінні та лінійну форму через неосновні. З останнього рівняння системи (4.5) (воно виділено) маємо х 1 = 20 + 0.5 · х 3 - х 6 . Підставляючи цей вислів в інші рівняння та в лінійну форму, отримаємо

З виразу лінійної форми випливає, що її максимальне значення ще не отримано, оскільки можливе збільшення Fза рахунок введення в основні змінної х 3 (вона має позитивний коефіцієнт). Вважаємо х 3 = min (∞; 30/0,25; 80/2; 20/0,5) =40.

Тут ми вперше зустрічаємося з двома положеннями, які потребують додаткових роз'яснень.

По-перше, хоча змінна х 3 і входить у вираз для х 1 (перше рівняння системи (4.6), але має позитивний коефіцієнт і за будь-якого зростання х 3 змінна х 1 не може стати негативною. Іншими словами, у першому рівнянні жодних обмежень на зростання змінної х 3 не накладається, тому умовно пишемо ∞. Умовимося надалі користуватися цим же позначенням, якщо змінна, знову введена в число основних, не входить до будь-якого рівняння системи обмеження.

По-друге, ми отримаємо два однакові мінімальні значення, рівні 40. Якщо х 3 = 40, то х 4 = 0 та х 5 = 0, тобто напрошується висновок, що замість однієї змінної потрібно перевести до числа неосновних відразу дві: х 4 та х 5 .Але число основних змінних має бути менше чотирьох. Для цього надходять у такий спосіб. Одну зі змінних ( х 4 або х 5.) залишають у числі основних, але при цьому її значення вважають рівним нулю, тобто отримане на наступному кроці базисне рішення виявляється виродженим. Залишимо, наприклад, х 4 серед основних змінних, а х 5 переведемо до числа неосновних.

4 крок. Основні змінні: х 1, х 2, х 3 , х 4; неосновні змінні: х5, х6. Виразимо основні змінні та лінійну форму Fчерез неосновні, почавши це вираз із четвертого рівняння системи (4.6). У результаті отримаємо

Так як вираз лінійної форми змінні х 5 та х 6 входять з негативним коефіцієнтами, то ніяке збільшення Fза рахунок цих змінних неможливо.

Відсутність на якомусь етапі симплексного методу у вираженні лінійної форми F, максимум якої шукається, неосновних змінних з позитивними коефіцієнтами є критерієм оптимальності.

Отже, на 4 етапі критерій оптимальності досягнуто і завдання вирішено. Оптимальним служить рішення (40; 20; 40; 0; 0; 0), при якому F max =140. Таким чином, для отримання найбільшого прибутку, що дорівнює 140 ден. од., з даних ресурсів необхідно отримати 40 одиниць продукції з сінокосів та 20 з ріллі. При цьому ресурси II, III та IV видів виявиться використаною повністю, а 40 од. І види залишаться невитраченими.

Приклад 4.2.Знайти максимум функції F = х 1 + 2 · х 2 при обмеженнях

Вводимо додаткові невід'ємні змінні х 3 ,х 4 ,х 5 ,х 6 і зводимо цю систему нерівностей до еквівалентної їй системи рівнянь

Введені додаткові змінні приймаємо за основні, тому що в цьому випадку базове рішення системи легко перебуває. Тоді х 1 та х 2 – неосновні змінні.

1 крок. Основні змінні: х 3 ,х 4 , х 5 , х 6; неосновні змінні; х 1 та х 2 . Виразивши основні змінні через неосновні, отримаємо

Отже, даному розбиття змінних на основні та неосновні відповідає базисне рішення (0; 0; - 2; - 4; 2; 6), яке є неприпустимим (дві змінні негативні), а тому воно не оптимальне. Від цього базового рішення перейдемо до покращеного.

Щоб вирішити, яку змінну слід перевести з неосновних до основних, розглянемо будь-яке з двох наявних рівнянь останньої системи з негативними вільними членами, наприклад, друге. Воно показує, що основні перемінні можна перевести х 1 та х 2 , оскільки в цьому рівнянні вони мають позитивні коефіцієнти (отже, при їх збільшенні, що станеться, якщо переведемо будь-яку з них до основних змінних, змінна х 4 збільшиться).

Спробуємо перевести до основних змінних х 1 . Щоб встановити, яку змінну слід перевести з основних у неосновні, знайдемо абсолютну величину найменшого відношення вільних членів системи до коефіцієнтів при х 1 , маємо х 1 = min (∞; 4/1; 2/1; ∞) = 2. Воно отримано з третього рівняння, що показує, що неосновні потрібно перекласти змінну х 5, яка у вихідному базисному рішенні позитивна.

Отже, отримане базисне рішення, як і вихідне, містить два негативні компоненти, тобто при переході до такого базисного рішення поліпшення не відбудеться.

Якщо ж перевести до основних змінних х 2 , то найменше відношення вільних членів до коефіцієнтів при х 2 складе х 2 - min (2/2; 4/1; ∞; 6/1) = 1. Воно отримано з першого рівняння, в якому вільний член від'ємний. Отже, перекладаючи х 2 в основні, а х 3 в неосновні змінні, ми отримаємо базисне рішення, в якому кількість негативних компонентів на одиницю менше, ніж у вихідному. Тому зупинимося на цій можливості: перекладаємо х 2 в основні, а х 3 у неосновні змінні; тоді виділеним виявиться перше рівняння.

2 крок. Основні змінні: х 2 ,х 4 ,х 5 ,х 6; неосновні змінні: х 1 та х 3 . Виразимо нові основні змінні через нові неосновні, починаючи це робити з виділеного на 1 кроці рівняння. В результаті отримаємо

Отже, маємо нове базисне рішення (0; 1; 0; -3; 3; 5), яке також є неприпустимим, а тому оптимальним. Але в ньому, як ми й передбачали, лише одна змінна негативна (а саме х 4).

Від отриманого базового рішення необхідно перейти до іншого. Розглянемо рівняння із негативним вільним членом, тобто. друге рівняння. Воно показує, що основні перемінні можна перевести х 1 та х 3 . Перекладемо в основні змінні х 1 . Знайдемо найменше з абсолютних величин відносин вільних членів системи до коефіцієнтів при х 1; маємо х 1 = min (∞; 3/1,5; 3/0,5; 5/0,5) = 2. Значить, у неосновні змінні потрібно перевести х 4 . Оскільки найменше ставлення отримано з другого рівняння, його виділяємо. У новому базисному рішенні не виявиться негативних компонент, т. е. воно є допустимим.

3 крок. Основні змінні: х 1 , х 2 , х 5 , х 6; неосновні змінні: х 3 , х 4 . Виразивши основні змінні через неосновні, отримаємо

Нове базисне рішення має вигляд (2; 2; 0; 0; 2; 4). Чи є воно оптимальним, можна встановити, якщо висловити лінійну форму через неосновні змінні аналізованого базисного рішення. Зробивши це, отримаємо. Таким чином, до лінійної форми звертаємося лише тоді, коли базисне рішення є допустимим. Оскільки ми шукаємо максимум лінійної форми, то отримане базисне рішення оптимальне.

Переводимо до основних змінну х 4 має більший позитивний коефіцієнт.

Знаходимо х 4 = min (∞; ∞; 2: (1/3); 4/(1/3)) = 6. Це найменше відношення отримано з третього рівняння системи, яке виділяємо. Воно показує, що за х 4 = 6 змінна х 5 = 0 і тому перейде до числа неосновних.

4 крок. Основні змінні: х 1 , х 2 , х 4 , х 6; неосновні змінні: х 3 , х 5 . Виразивши основні змінні через неосновні, отримаємо

Лінійна форма, виражена через ті ж неосновні змінні, набуде вигляду. Отже, базисне рішення (6; 4; 0; 6; 0; 2), якого ми перейшли, перестав бути оптимальним.

Збільшення лінійної форми можливе при переході до нового базисного рішення, в якому змінна х 3 є основною. Знаходимо х 3 = min (∞; ∞; с; 2/1) = 2. Це найменше відношення отримано з четвертого рівняння системи і показує, що при х 3 = 2 змінна х 6 = 0 і перетворюється на число неосновных.

5 крок. Основні змінні: х 1 , х 2 , х 3 , х 4 неосновні змінні х 5 ,х 6 .Виразивши основні змінні через неосновні, отримаємо

Лінійна форма, виражена через неосновні змінні нового базисного рішення, має вигляд . Критерій оптимальності для максимізації лінійної форми виконаний. Отже, базисне рішення (8; 6; 2; 10, 0; 0) є оптимальним, а максимум лінійної форми F max = 20.

4.5 Графічне розв'язання задач

лінійного програмування

Графічний спосіб розв'язання задач лінійного програмування доцільно використовувати для:

Розв'язання задач із двома змінними, коли обмеження виражені нерівностями;

Розв'язання задач з багатьма змінними за умови, що в їхньому канонічному записі міститься не більше двох вільних змінних.

Запишемо завдання лінійного програмування з двома змінними:

цільова функція:

обмеження:

Кожна з нерівностей (4.8) системи обмежень задачі геометрично визначає напівплощину відповідно до граничних прямих ; . У тому випадку, якщо система нерівностей (4.8) спільна, область її розв'язків є безліч точок, що належать усім зазначеним напівплощин. Так як безліч точок перетину даних напівплощин - опукле, то областю допустимих рішень є опукла множина, яка називається багатокутником рішень. Сторони цього багатокутника лежать на прямих, рівняння яких виходять із вихідної системи обмежень заміною знаків нерівностей на рівні знаки.

Областю допустимих розв'язків системи нерівностей (4.8) може бути:

Випуклий багатокутник;

Випукла багатокутна необмежена область;

Порожня область;

Відрізок;

Єдина точка.

Цільова функція (4.7) визначає на площині сімейство паралельних прямих, кожній з яких відповідає певне значення Z.

Вектор з координатами і , перпендикулярний цим прямим, вказує напрямок якнайшвидшого зростання Z, а протилежний вектор - напрямок зменшення Z.

Якщо в одній і тій же системі координат зобразити область допустимих розв'язків системи нерівностей (4.8) і сімейство паралельних прямих (4.7), то завдання визначення максимуму функції Z зведеться до знаходження в допустимій ділянці точки, через яку проходить пряма із сімейства Z = const, і яка відповідає найбільшому значенню параметра Z.

Ця точка існує тоді, коли багатокутник рішень не порожній і цільова функція на ньому обмежена зверху. За зазначених умов в одній з вершин багатокутника розв'язків цільова функція набуває максимального значення.

Для визначення даної вершини побудуємо лінію рівня, що проходить через початок координат і перпендикулярну вектору , і пересуватимемо її в напрямку вектора доти, доки вона не торкнеться останньої крайньої (кутової) точки багатокутника рішень. Координати зазначеної точки визначають оптимальний план даної задачі.

Рисунок 4.1 - Оптимум функції Z досягнемо у точці А

Рисунок 4.2 - Оптимум функції Z досягається у будь-якій точці [АВ]

Закінчуючи розгляд геометричної інтерпретації завдання (4.7) - (4.8), зазначимо, що з знаходженні її вирішення можуть трапитися випадки, зображені на рис. 4.1 – 4.4. Рисунок 4.1 характеризує такий випадок, коли цільова функція набуває максимального значення в єдиній точці А. З малюнка 4.2 видно, що максимальне значення цільова функція набуває у будь-якій точці відрізка АВ.

Рисунок 4.3 - Оптимум функції Z недосяжний

Малюнок 4.4 - Область допустимих рішень - пуста область

На малюнку 4.3 зображено випадок, коли максимум недосяжний, а малюнку 4.4 - випадок, коли система обмежень завдання несовместна. Зазначимо, що знаходження мінімального значення Z при даній системі обмежень відрізняється від знаходження її максимального значення при тих же обмеженнях лише тим, що лінія рівня Z пересувається не в напрямку вектора, а в протилежному напрямку. Таким чином, зазначені вище випадки, що зустрічаються при знаходженні максимального значення цільової функції, мають місце і щодо її мінімального значення.

Для практичного розв'язання задачі лінійного програмування (4.7) – (4.8) на основі її геометричної інтерпретації необхідно наступне.

1.Побудувати прямі, рівняння яких утворюються внаслідок заміни в обмеженнях (4,4) знаків нерівностей на знаки рівностей.

2.Знайти напівплощини, що визначаються кожним з обмежень задачі.

3.Визначити багатокутник рішень.

4.Побудувати вектор.

5. Побудувати пряму, яка проходить через початок координат і перпендикулярну до вектора.

6.Передвигать пряму у напрямі вектора , у результаті знаходять точку (точки), у якій цільова функція приймає максимальне значення, або встановлюють необмеженість функції зверху безлічі планів.

7.Визначити координати точки максимуму функції та обчислити значення цільової функції у цій точці.

приклад 4.3.Підприємство виготовляє два види продукції П та Р, яка надходить до оптового продажу. Для виробництва продукції використовують два види сировини А та Б. Максимально можливі запаси сировини на добу становитимуть 9 та 13 одиниць відповідно. Витрата сировини виду А на виробництво продукції П і Р складуть 2 та 3 одиниці відповідно, виду Б 3 та 2 одиниці. Досвід роботи показав, що добовий попит продукції П ніколи не перевищує попиту на продукцію Р більш ніж на 1 одиницю. Крім того, відомо, що попит на продукцію Р ніколи не перевищує 2 одиниці на добу. Оптові ціни одиниці виробленої продукції рівні 3 одиниці для П, і 4 одиниці для Р. Яка кількість продукції кожного виду має зробити підприємство, щоб прибуток від реалізації був максимальним. Розв'язати задачу геометричним способом.

Рішення. Побудуємо багатокутник розв'язків (рис. 7.5). Для цього в системі координат X 1 OX 2 на площині зобразимо граничні прямі:

Взявши якусь точку, наприклад, початок координат, встановимо, яку напівплощину визначає відповідну нерівність. Напівплощини, що визначаються нерівностями, на рис. 7.5 показано стрілками. Областю рішень є багатокутник OABCD.

Для побудови прямий будуємо вектор-градієнт і через точку 0 проводимо пряму перпендикулярну йому. Побудовану пряму Z = 0 переміщуємо паралельно собі у напрямку вектора . З рис. 4.5 випливає, що стосовно багатокутника рішень опорної ця пряма стає в точці С, де функція набуває максимального значення. Точка лежить на перетині прямих L 1 і Z 3 . Для визначення її координат вирішимо систему рівнянь:

Оптимальний план задачі = 24; =1,4. Підставляючи значення і лінійну функцію, отримаємо:

3 2,4 + 4 1,4 = 12,8.

Отримане рішення означає, що обсяг виробництва продукції П повинен дорівнювати 2,4 од., а продукції Р - 1,4 од. Дохід, одержуваний у цьому випадку, становитиме: Z = 12,8 д. е.

Рисунок 4.5 - Розв'язання задачі лінійного програмування геометричним способом

5. ПОДВІЙНІ ЗАВДАННЯ

Складання двоїстої задачі. Розглянемо дві задачі лінійного програмування:

Максимізувати функцію

при обмеженнях

Мінімізувати функцію

при обмеженнях

Ці завдання мають такі властивості:

1. В одному завданні шукається максимум лінійної форми, а в іншому – мінімум.

2 °. Коефіцієнти при змінних у лінійній формі одного завдання є вільними членами системи обмежень іншого завдання, навпаки, вільні члени системи обмежень одного завдання – коефіцієнтами при змінних у лінійній формі іншого завдання.

3 °. У кожному завданні система обмежень задається у вигляді нерівностей, причому всі вони одного сенсу, а саме: при знаходженні максимуму лінійної форми ці нерівності мають вигляд, а при знаходженні мінімуму – вид

4 °. Коефіцієнти при змінних системах обмежень описуються матрицями

які є транспонованими щодо один одного.

5 °. Число нерівностей у системі обмежень однієї задачі збігається з числом змінних іншого завдання.

6 е. Умови невід'ємності змінних зберігаються в обох задачах.

Дві задачі лінійного програмування, які відповідають зазначеним вище умовам, називаються симетричними взаємно двоїстими завданнями. Ми вивчатимемо лише симетричні двоїсті завдання, а тому називатимемо їх коротше – двоїстими завданнями.

Таким чином, кожній задачі лінійного програмування можна поставити у відповідність подвійне їй завдання. Початкове завдання називатимемо вихідним (або прямим). Пряме і двоїсте їй завдання, узяті разом, утворюють пару взаємно двоїстих завдань, причому будь-яку з них можна розглядати як вихідну, тоді інша виявиться двоїстою їй.

Зі сказаного випливають такі правила складання завдання, двоїстої по відношенню до вихідної:

1. Наводять усі нерівності системи обмежень вихідного завдання до нерівностей одного змісту: якщо у вихідному завданні шукається максимум лінійної форми – до вигляду ≤, якщо мінімум – до виду ≥. Для цього нерівності, у яких ця вимога не виконується, множать на -1.

2. Виписують матрицю А коефіцієнтів при змінних вихідної задачі, отриманих після перетворення п. 1, і становлять матрицю А, транспоновану щодо матриці А.

3. Складають систему обмежень двоїстої задачі, взявши як коефіцієнти при змінних елементи матриці А", а як вільні члени – коефіцієнти при змінних у лінійній формі вихідного завдання, і записують нерівності протилежного сенсу порівняно з нерівностями, отриманими в п. 1.

4. Складають лінійну форму двоїстого завдання, прийнявши за коефіцієнти при змінних вільні члени системи обмежень вихідного завдання, отримані у п. 1.

5. Вказують, що необхідно знайти при вирішенні двоїстої задачі, а саме: мінімум лінійної форми, якщо у вихідному завданні шукається максимум, і максимум, якщо у вихідному завданні шукається мінімум.

6. Записують умову невід'ємності змінних двоїстої задачі.

Приклад 5.1. Скласти завдання, подвійне наступному: знайти максимум функції при обмеженнях

Третя нерівність системи (*) не задовольняє п. 1 правил складання двоїстої задачі. Тому помножимо його на -1:

Для полегшення складання двоїстої задачі краще користуватися розширеною матрицею, в яку поряд з коефіцієнтами при змінних системи обмежень вихідної задачі запишемо вільні члени і коефіцієнти при змінних у лінійній формі, виділивши для цієї мети додаткові стовпець і рядок. Матрицю транспонуємо і, використовуючи транспоновану матрицю /, складаємо задачу подвійну даної.

Подвійне завдання зводиться до знаходження мінімуму функції при обмеженнях

Основні теореми двоїстості

Теорія двоїстості в лінійному програмуванні будується наступних основних теоремах.

Теорема 1. Якщо одне із завдань лінійного програмування має кінцевий оптимум, то і подвійна до неї також має кінцевий оптимум, причому оптимальні значення лінійних форм обох завдань збігаються, тобто F max = Z min або F min = Z max. Якщо ж лінійна форма однієї з двоїстих завдань не обмежена, то умови іншого завдання суперечливі.

Перш ніж сформулювати наступну теорему, встановимо відповідності між змінними у вихідному та двоїстому завданнях.

При вирішенні симплексним методом вихідного завдання для зведення системи нерівностей до еквівалентної їй системи рівнянь потрібно ввести додаткових невід'ємних змінних (за кількістю нерівностей у системі обмежень) де i = 1, 2,…,т означає номер нерівності, в яку було введено додаткову змінну .

Система обмежень двоїстої задачі складається з п нерівностей, що містять змінних. Якщо розв'язувати це завдання симплексним методом, слід ввести п додаткових неотрицательных змінних де j = 1, 2,…,т означає номер нерівності системи обмежень двоїстої завдання, у якому була введена додаткова змінна .

Встановимо таку відповідність між змінними у вихідному та двоїчому завданнях:

Іншими словами, кожною початковою змінною вихідною
Завдання x j (j = 1,2 ,…, п) ставиться у відповідність додаткова змінна , введена в j - e нерівність двоїстої задачі, а кожної додаткової змінної вихідної задачі (i = 1,2,…, т), введеної в i- e нерівність вихідної задачі, – первісна змінна двоїстої задачі.

Теорема 2 . Компоненти оптимального розв'язання однієї із завдань (прямої чи двоїстої) дорівнюють абсолютним величинам коефіцієнтів при відповідних змінних у вираженні лінійної форми іншого завдання (двійної чи прямої) при досягненні нею оптимуму та за умови, що отримане оптимальне рішення не є виродженим.

З теорем 1 і 2 випливає, що якщо вирішити одну з взаємно двоїстих завдань, тобто знайти її оптимальне рішення та оптимум лінійної форми, то можна записати оптимальне рішення та оптимум лінійної форми іншого завдання.

Приклад 5.2. Розв'язати симплексним методом пряме та двоїсте завдання, наведені в попередньому прикладі.

Розв'язання прямої задачі. Зведемо систему обмежень нерівностей (див. с. 268) до системи рівнянь, ввівши невід'ємні додаткові змінні:

Додаткові змінні х 3 , х 4 , х 5 , х 6 приймемо за основні на кроці рішення.

1 крок. Основні змінні: х 3, х 4, х 5, х 6; неосновні змінні: х1, х2. Виразимо основні змінні через неосновні (лінійну форму на цьому етапі рішення не розглядаємо, оскільки відповідне базове рішення не є допустимим):

Для отримання допустимого базисного рішення змінну переведемо до основних. Знаходимо = min (2/1; ∞; 1/1; 5/1) = 1. При цьому змінна х 5переходить у неосновні.

2 крок. Основні змінні: х 1, х 3, х 4, х 6 неосновні змінні; х 2 , х 5. Виразимо основні змінні та лінійну форму через неосновні:

Перекладемо в основні змінну х 5. Вважаючи х 5=min(∞; 1/1; ∞; 4/1) = 1, укладаємо, що змінну х 3 потрібно перевести в неосновні.

3 крок. Основні змінні: х 1, х 4 х 5 х 6 неосновні змінні х 3 х 2 . Маємо

Змінну х 2 переводимо в основні. Знаходимо х 2 = min (∞; ∞;∞; 1/1) = 1. Тоді змінна х 6 перетворюється на неосновні.

4 крок. Основні змінні:: х 1 , х 2 , х 4, х 5,; неосновні змінні: х2, х6. Маємо

Критерій оптимальності виконано. Оптимальне рішення має вигляд (4; 1; 0; 5; 4; 0); при цьому рішенні Fmax = 13.

Продовження прикладу 5.1. Систему обмежень двоїстої задачі зводимо до системи рівнянь:

Додаткові змінні y 5 y 6 приймемо за основні на 1 кроці рішення.

1 крок. Основні змінні: y 5 , y 6; неосновні змінні: y 1 , 2 , 3 , 4 . Виразимо основні змінні через неосновні:

Переведемо до основних змінних у 4 . Знаходимо у 4 = mm (3/1: 1/1 = 1. Змінна y 6 перетворюється на неосновні.

2 крок. Основні змінні: у 4 , y 5 неосновні змінні: y 1 , 2 , 3 , 6 . Маємо

Змінну y1 переведемо в основні. Оскільки y 1 = min (∞; 2/3) = 2/3, то змінна y 5 перетворюється на неосновные.

3 крок. Основні змінні y 1, у 4, неосновні змінні: у 2, у 3, y 5, у 6. Оскільки відповідне базисне рішення завдання є допустимим, то виразимо через неосновні змінні як основні, а й лінійну форму:

Критерій оптимальності (для випадку мінімізації лінійної форми) виконано. Оптимальне рішення має вигляд (2/3; 0; 0; 7/3; 0; 0), причому Z min = 13.

Розв'язавши двоїсте завдання, переконуємось у справедливості першої частини теореми 1: подвійне завдання теж має кінцевий оптимум, причому Z min = = Fmax = 13.

Переконаємося, що справедливе також і затвердження теореми 2. Для цього запишемо змінні прямі та двоїсті завдання, дотримуючись їх відповідності;

Лінійну форму, отриману на останньому кроці розв'язання двоїстої задачі, виразимо через усі змінні цієї задачі:

Розглядаючи коефіцієнти при змінних y j у цій лінійній формі та враховуючи їх відповідність з коефіцієнтами при змінних x i ,отримаємо рішення (4; 1; 0; 5; 4; 0), що збігається з оптимальним рішенням прямої задачі.

Зауваження. Розв'язавши пряме завдання, можна відразу отримати рішення двоїстої задачі. Якщо виразити лінійну форму F, отриману на 4 кроці розв'язання прямої задачі, через усі змінні цієї задачі, то отримаємо

На підставі теореми 2, враховуючи відповідність між змінними у прямій та двоїстій задачах і взявши абсолютну величину коефіцієнтів при змінних, знайдемо оптимальне рішення двоїстої задачі (2/3; 0; 0; 7/3; 0; 0). У цьому Z min =F max = 13.

6 ТРАНСПОРТНЕ ЗАВДАННЯ

Цьому випадку відповідає взаємна суперечливість обмежень, що входять до завдання.

2) Допустиме безліч - опуклий обмежений багатогранник.

Допустима множина - опукла необмежена багатогранна множина.

Два останні випадки досить легко уявити у дво- або тривимірному вимірі. У просторі більшої розмірності поняття багатогранника (багатогранної множини) вводиться абстрактно як перетин гіперплощин і гіперпівплощин, що визначаються відповідними лінійними рівняннями та нерівностями, що входять до складу обмежень задачі. Характерною властивістю багатогранника є наявність у ньому особливих точок. вершин.

Можливі випадки оптимальних розв'язків (планів) задачі лінійного програмування.

1) Завдання не має оптимальних рішень.

Даний випадок може виникнути: або тоді, коли допустима безліч рішень порожня ("ні з чого вибирати" оптимальний план),

або коли допустима множина є необмеженою багатогранною множиною, і цільова функція на ньому необмежено зростає (якщо L max) або необмежено зменшується (при Lmin).

2) Завдання має єдине Рішення(Єдиний оптимальний план).

Це рішення обов'язково збігається з однією з вершин допустимої множини.

3) Завдання має безлічоптимальних рішень, задане деякою лінійною освітою – рубом, гранню, гіпергранню тощо. Серед точок цієї лінійної освіти є і вершини допустимої множини.

Таким чином, основне твердження теорії лінійного програмування, що зрештою визначає специфічні способи його вирішення, можна сформулювати наступним чином:

Якщо завдання лінійного програмування має хоча б один оптимальний план, його слід шукати серед вершин допустимого безлічі рішень.

У наступному параграфі розглянуті загальні положення будуть проілюстровані з прикладу завдання лінійного програмування з двома змінними.

1. Графоаналітичний спосіб розв'язання задач лінійного програмування

Графоаналітичний (графічний) спосіб розв'язання задач лінійного програмування зазвичай використовується для вирішення задач з двома змінними, коли обмеження виражені нерівностями, а також задач, які можуть бути зведені до таких завдань.

Нехай завдання лінійного програмування має вигляд:

(1.7)

де з 1 , з 2 , а i 1 , а i 2 , b i - задані дійсні числа; знаки у нерівностях довільні; цільова функція або максимізується або мінімізується.

Кожна з нерівностей (1.7) системи обмежень задачі геометрично визначає напівплощину відповідно до граничних прямих
;i=1,…,m. У тому випадку, якщо система нерівностей (1.7) спільна, допустима область розв'язання задачі є безліч точок, що належать усім зазначеним напівплощин. Так як безліч точок перетину даних напівплощин – опукле, то областю допустимих значень є опукла множина, яку називають багатокутникомрішень. Сторони цього багатокутника лежать на прямих, рівняння яких виходять із вихідної системи обмежень заміною знаків нерівностей на рівні знаки.

Безліч допустимих рішень для даної приватної задачі може бути:

порожня область;

опуклий багатокутник, включаючи вироджені випадки - відрізок та єдину точку;

опукла багатокутна необмежена область, включаючи вироджені випадки - промінь та пряму.

Практична реалізація розв'язання задачі лінійного програмування (1.6) – (1.7) на основі її геометричної інтерпретації включає наступні етапи:

1. Побудувати прямі, рівняння яких утворюються внаслідок заміни в обмеженнях (1.7) знаків нерівностей на знаки рівностей.

2. Знайти напівплощини, що визначаються кожним з обмежень.

Відповідна напівплощина може бути знайдена підстановкою в нерівність координат якоїсь «простої» точки - (0,0), (0,1) або (1,0). Головне – щоб ця точка не належала межі напівплощини. Якщо після підстановки нерівність виявиться справедливою, то вибирається та напівплощина, де міститься ця точка. Якщо нерівність не справедлива, то вибирається альтернативна напівплощина.

3. Визначити багатокутник рішень, як перетин знайдених напівплощин.

4. Побудувати градієнт цільової функції, тобто. вектор
координатами якого служать коефіцієнти цільової функції L.

Цей вектор визначає напрямок якнайшвидшого зростання цільової функції.

5. Побудувати ряд ліній рівня цільової функції L, тобто. прямих перпендикулярних градієнту L.

При цьому побудову ліній рівня слід вести в напрямку градієнта, якщо вирішується завдання на максимум, і в протилежному напрямку (у напрямку «антиградіенту»), якщо завдання вирішується на мінімум. В результаті відзначається точка (точки), в якій лінії рівня в останній раз стосуються допустимої множини.
Якщо допустима множина необмежена, то точки останнього дотику може і не бути. Лінії рівня йдуть у нескінченність, відповідно значення
або

і завдання не має оптимальних планів.

Визначити координати зазначеної точки аналітично, розв'язуючи відповідну систему лінійних рівнянь. Потім обчислити значення цільової функції у цій точці. Тим самим визначається оптимальний план і оптимальне значення цільової функції завдання.

Закінчуючи розгляд геометричної інтерпретації завдання (1.6) - (1.7), зазначимо, що при знаходженні її рішення можуть трапитися випадки, зображені на рис. 1.1 – 1.3. Мал. 1.1 характеризує такий випадок, коли цільова функція набуває оптимального значення в єдиній точці А, однієї з вершин допустимої множини. На рис. 1.2 оптимальне значення цільова функція набуває у будь-якій точці відрізка АВ. На рис. 1.3 зображено випадок, коли оптимальне значення цільової функції є недосяжним. LМал. 1.1. Оптимум функції

досягнемо в точці А LМал. 1.2. Оптимум функції досягається в будь-якій точці відрізка

АB LМал. 1.3. Оптимум функції