Comment trouver la solution optimale pour le processus de production. Quelle solution peut être considérée comme optimale ? Méthode graphique-analytique pour résoudre des problèmes de programmation linéaire

Il convient de noter que les méthodes de résolution des problèmes de programmation linéaire comprennent non pas à l’économie, mais aux mathématiques et à l’informatique. Dans le même temps, l'économiste doit offrir les conditions de dialogue les plus confortables avec le logiciel approprié. À leur tour, de telles conditions ne peuvent être assurées que par des environnements de développement dynamiques et interactifs qui disposent dans leur arsenal d'un ensemble de bibliothèques nécessaires à la résolution de tels problèmes. L'un des environnements de développement logiciel est sans aucun doute Python.

Formulation du problème

Les publications envisageaient des solutions aux problèmes d'optimisation directe à l'aide de la méthode de programmation linéaire et suggéraient un choix raisonnable du solveur scipy. optimiser.

Or, on sait qu'à chaque problème de programmation linéaire correspond un problème dit distingué (dual). Dans celui-ci, par rapport au problème direct, les lignes se transforment en colonnes, les inégalités changent de signe, au lieu d'un maximum, un minimum est recherché (ou vice versa, au lieu d'un minimum, un maximum est recherché). La tâche duale au dual est la tâche originelle elle-même.

La résolution de ce double problème est très importante pour analyser l’utilisation des ressources. Dans cette publication, il sera prouvé que les valeurs optimales des fonctions objectives dans les problèmes original et dual coïncident (c'est-à-dire que le maximum dans le problème original coïncide avec le minimum dans le dual).

Les valeurs optimales des coûts de matériel et de main d'œuvre seront évaluées par leur contribution à la fonction objectif. Le résultat sera des « estimations objectivement déterminées » des matières premières et de la main-d’œuvre qui ne coïncident pas avec les prix du marché.

Solution du problème direct du programme de production optimal

Compte tenu du haut niveau de formation mathématique de la grande majorité des utilisateurs de cette ressource, je ne présenterai pas d'équations d'équilibre avec des restrictions supérieures et inférieures et l'introduction de variables supplémentaires pour passer aux égalités. Je donnerai donc immédiatement les désignations des variables utilisées dans la solution :
N – nombre de types de produits fabriqués ;
m – nombre de types de matières premières utilisées ;
b_ub - vecteur de ressources disponibles de dimension m ;
A_ub est une matrice de dimension m×N dont chaque élément est la consommation d'une ressource de type i pour la production d'une unité de produit de type j ;
c est le vecteur de profit de la production d'une unité de chaque type de produit ;
x – les volumes requis de produits fabriqués de chaque type (plan de production optimal) garantissant un profit maximum.

Fonction d'objectif
maxF(x)=c×x

Restrictions
A×x≤b

Valeurs numériques des variables :
N=5 ; m = 4 ; b_ub = ; A_ub = [, , ,]; c = .

Tâches
1. Trouvez x pour assurer un profit maximum
2. Recherchez les ressources utilisées lors de l'exécution de l'étape 1
3. Recherchez les ressources restantes (le cas échéant) lors de l'exécution de l'étape 1

Pour déterminer le maximum (par défaut, le minimum est déterminé, les coefficients de la fonction objectif doivent être écrits avec un signe négatif c = [-25, -35,-25,-40,-30] et ignorer le signe moins devant le profit.

Notations utilisées pour afficher les résultats :
X– un tableau de valeurs variables qui fournissent le minimum (maximum) de la fonction cible ;
mou– valeurs de variables supplémentaires. Chaque variable correspond à une contrainte d'inégalité. Une valeur variable de zéro signifie que la contrainte correspondante est active ;
succès– Vrai, si la fonction a réussi à trouver la solution optimale ;
statut– statut de la décision :
0 – la recherche de la solution optimale s'est terminée avec succès ;
1 – la limite du nombre d'itérations a été atteinte ;
2 – le problème n’a pas de solution ;
3 – la fonction objectif n’est pas limitée.
lente– nombre d'itérations effectuées.

Listage de la solution au problème d'optimisation directe

#!/usr/bin/python # -*- codage : utf-8 -*- import scipy depuis scipy.optimize import linprog # chargement de la bibliothèque LP c = [-25, -35,-25,-40,-30] # liste des coefficients de la fonction objectif b_ub = # liste des volumes de ressources A_ub = [, # matrice de valeurs de ressources spécifiques, , ] d=linprog(c, A_ub, b_ub) # recherche d'une solution pour key,val in d.items(): print(key ,val) # sortie de la solution if key=="x": q=#ressources utilisées print("A_ub*x",q) q1= scipy.array(b_ub)-scipy.array (q) #ressources restantes print(" b_ub-A_ub*x", q1)

Résultats de la résolution du problème
lente 3
statut 0

succès Vrai
x [ 0. 0. 18.18181818 22.72727273 150. ]
A_ub*x
b_ub-A_ub*x [0.0.0.90.90909091]
amusant -5863.63636364
mou [0. 0. 0. 90.90909091]

conclusions

1. Le plan optimal pour les types de produits a été trouvé
2. Utilisation réelle des ressources trouvée
3. Le reste du quatrième type de ressource inutilisé a été trouvé [ 0. 0 0.0 0.0 90.909]
4. Il n'est pas nécessaire d'effectuer les calculs selon l'étape 3, puisque le même résultat est affiché dans la variable slack

Solution du double problème sur le programme de production optimal

Le quatrième type de ressource dans la tâche directe n'est pas entièrement utilisé. La valeur de cette ressource pour l'entreprise s'avère alors inférieure à celle des ressources qui limitent la production, et l'entreprise est prête à payer un prix plus élevé pour l'acquisition de ressources qui augmentent les profits.

Introduisons un nouvel objectif pour la variable souhaitée x en tant que prix « fictif » qui détermine la valeur d'une ressource donnée par rapport au profit de la vente de produits manufacturés.

C – vecteur de ressources disponibles ;
b_ub est le vecteur de profit de la production d'une unité de chaque type de produit ;
A_ub_T – matrice transposée A_ub.

Fonction d'objectif
minF(x)=c×x

Restrictions
A_ub_T ×x≥ b_ub

Valeurs numériques et relations pour les variables :
c = ; A_ub_T transpose(A_ub); b_ub = .

Tâche:
Trouvez x indiquant la valeur pour le producteur de chaque type de ressource.

Fonctionnalités de la solution avec la bibliothèque scipy. optimiser
Pour remplacer les restrictions d'en haut par des restrictions d'en bas, il faut multiplier les deux parties de la contrainte par moins un – A_ub_T ×x≥ b_ub... Pour cela, écrivez les données initiales sous la forme : b_ub = [-25, -35,-25,-40,-30] ; A_ub_T =- scipy.transpose(A_ub).

Listing de la solution au problème de double optimisation

#!/usr/bin/python # -*- codage : utf-8 -*- importer scipy depuis scipy.optimize import linprog A_ub = [, , , ] c= b_ub = [-25, -35,-25,- 40,-30] A_ub_T =-scipy.transpose(A_ub) d=linprog(c, A_ub_T, b_ub) pour key,val dans d.items() : print(key,val)

Résultats de la résolution du problème
lenteur 7
message L'optimisation s'est terminée avec succès.
amusant 5863.63636364
x [ 2,27272727 1,81818182 6,36363636 0. ]
mou [5.45454545 2.27272727 0. 0. 0. ]
statut 0
succès Vrai

conclusions

Le troisième type de ressource a la plus grande valeur pour le fabricant, ce type de ressource doit donc être acheté en premier, puis les premier et deuxième types. Le quatrième type de ressource a une valeur nulle pour le fabricant et est acheté en dernier.

Résultats de la comparaison des problèmes directs et duaux

1. Le double problème étend les capacités de planification de produits, mais en utilisant scipy. L'optimisation est résolue en deux fois plus d'itérations directes.
2. La variable slack affiche des informations sur l'activité des contraintes sous forme d'inégalités, qui peuvent être utilisées, par exemple, pour analyser les bilans de matières premières.
3. Le problème direct est un problème de maximisation, et le problème dual est un problème de minimisation, et vice versa.
4. Les coefficients de la fonction objectif dans le problème direct sont des contraintes dans le problème dual.
5. Les contraintes du problème direct deviennent des coefficients de la fonction objectif du problème dual.
6. Les signes d’inégalités en matière de restrictions s’inversent.
7. La matrice du système d’égalités est transposée.

Liens L'optimisation des modèles linéaires dans MS Excel est effectuée méthode simplexe- recherche ciblée de solutions de référence à un problème de programmation linéaire. L'algorithme de la méthode simplexe revient à construire un polyèdre convexe dans un espace multidimensionnel, puis à énumérer ses sommets pour trouver une valeur extrême fonction objectif.

Des moyens efficaces programmation linéaire constituent la base de la programmation entière et non linéaire pour résoudre des problèmes d'optimisation plus complexes. Ces méthodes nécessitent cependant des temps de calcul plus longs.

Les conférences suivantes discuteront en détail d'exemples de résolution de problèmes d'optimisation typiques et de prise de décisions de gestion à l'aide du complément MS Excel « Rechercher une solution ». Les tâches qui sont mieux résolues par cet outil ont trois propriétés principales :

• il y a un seul objectif, fonctionnellement lié à d'autres paramètres du système, qui doit être optimisé (pour trouver son maximum, son minimum ou une certaine valeur numérique) ;
• il existe des restrictions, généralement exprimées sous forme d'inégalités (par exemple, le volume de matières premières utilisées ne peut pas dépasser le stock de matières premières dans l'entrepôt, ou la durée de fonctionnement d'une machine par jour ne doit pas dépasser 24 heures moins la maintenance temps);
• il existe un ensemble de valeurs de variables d'entrée qui influencent les valeurs et les restrictions optimisées.

Les paramètres des tâches sont limités aux indicateurs limites suivants :

• nombre d'inconnues – 200 ;
• nombre de restrictions formelles sur les inconnues – 100 ;
• le nombre de conditions limites pour les inconnues est de 400.

L'algorithme de recherche de solutions optimales comprend plusieurs étapes :

• travail préparatoire;
• déboguer la solution ;
• analyse des solutions.

La séquence des travaux préparatoires nécessaires effectués lors de la résolution de problèmes de modélisation économique et mathématique à l'aide de MS Excel est présentée dans le schéma fonctionnel de la figure 1.6.

Riz. 1.6.

Sur les cinq points du plan de travail préparatoire, seul le cinquième point est formalisable. Le reste du travail requiert de la créativité – et différentes personnes peuvent le faire de différentes manières. Expliquons brièvement l'essence du libellé des éléments du plan.

Lors de la définition du problème, les coefficients cibles et les coefficients normalisés sont connus. Dans l'exemple précédent, les coefficients formant la fonction objectif étaient les valeurs de profit normalisé par étagère de type ( ) et un type d'étagère ( ). Les coefficients normalisés étaient les normes de consommation de matière et de temps machine par étagère de chaque type. La matrice ressemblait à ceci :

De plus, les valeurs des ressources sont toujours connues. Dans l'exemple précédent, il s'agissait d'un approvisionnement d'une semaine en cartes et de la possibilité d'utiliser le temps machine : , . Souvent, dans les problèmes, les valeurs des variables doivent être limitées. Par conséquent, il est nécessaire de déterminer les limites inférieure et supérieure de la plage de leurs modifications.

Ainsi, dans la boîte de dialogue du programme d'optimisation « Rechercher une solution », nous devons définir l'algorithme cible suivant :

La fonction cible est égale au produit du vecteur des valeurs des variables souhaitées par le vecteur des coefficients cibles

Les coefficients normalisés pour le vecteur des valeurs de variables requises ne doivent pas dépasser la valeur du vecteur de ressources donné

Les valeurs des variables doivent être dans les limites spécifiées du nombre d'éléments initiaux du système

Nombre d'éléments initiaux du système

Nombre de types de ressources spécifiés

Le débogage de la solution est nécessaire lorsque le programme affiche un message concernant des résultats négatifs (Figure 1.7) :

Riz. 1.7.

• si une solution acceptable n'est pas obtenue, ajustez le modèle de données source ;
• si non reçu solution optimale, puis introduisez des restrictions supplémentaires.

Les enjeux du programme solution optimale uniquement pour un modèle du problème réel, et non pour une solution au problème lui-même. Lors de la construction du modèle, diverses hypothèses simplificatrices ont été formulées concernant la situation réelle. Cela a permis de formaliser le processus, affichant approximativement des relations quantitatives réelles entre les paramètres du système et l'objectif. Et si les paramètres réels diffèrent de ceux inclus dans le modèle, comment la solution changera-t-elle ? Pour le savoir, avant de prendre une décision de gestion, une analyse de la solution modèle est réalisée.

Analyse solution optimale, intégré au programme, représente l'étape finale de la modélisation mathématique des processus économiques. Il permet de vérifier plus en profondeur la conformité du modèle avec le processus, ainsi que la fiabilité de la solution optimale. Il est basé sur des données solution optimale et les rapports publiés dans le cadre de la « Recherche d'une solution ». Mais cela n’exclut ni ne remplace l’analyse traditionnelle du plan d’un point de vue économique avant de prendre une décision de gestion.

L'analyse économique poursuit les objectifs suivants :

• détermination des conséquences possibles sur le système dans son ensemble et ses éléments lors de la modification d'un paramètre du modèle ;
• évaluation de la stabilité du plan optimal aux changements des paramètres individuels du problème : s'il n'est pas stable aux changements de la plupart des paramètres, la garantie de sa mise en œuvre et de l'atteinte de l'optimum calculé est réduite ;
• effectuer des calculs de variantes et obtenir de nouvelles options de plan sans résoudre le problème à partir de la base d'origine à l'aide d'ajustements.

Les méthodes d'analyse possibles sont présentées dans le diagramme de la figure 1.8.

Après avoir obtenu la solution optimale, celle-ci est analysée sur la base des rapports reçus. Analyse de stabilité- étude de l'influence des changements des paramètres individuels du modèle sur les indicateurs de la solution optimale. Analyse des limites- analyse des changements admissibles dans le plan optimal, dans lequel le plan reste optimal.

Compte tenu de la responsabilité d’accepter des mesures économiques décision de gestion, le manager doit s'assurer que le plan optimal qui en résulte est le seul correct. Pour ce faire, à partir du modèle, il est nécessaire d'obtenir des réponses aux questions suivantes :

• "ce qui se passe si…"
• "que faut-il pour..."

L'analyse pour répondre à la première question est appelée analyse des variantes; L'analyse pour répondre à la deuxième question s'appelle solutions personnalisées.

L'analyse des variantes peut être des types suivants :

• Paramétrique- l'analyse, qui consiste à résoudre un problème pour différentes valeurs d'un certain paramètre.
• Analyse structurelle- lorsqu'une solution à un problème d'optimisation est recherchée sous une structure de contraintes différente.
• Analyse multicritère est une solution à un problème utilisant différentes fonctions objectifs.
• Analyse avec des données initiales conditionnelles- lorsque les données initiales utilisées pour résoudre un problème dépendent du respect de conditions complémentaires.

Après l'analyse, les résultats doivent être présentés sous forme graphique et un rapport doit être rédigé avec des recommandations pour prendre des décisions en tenant compte de la situation économique spécifique.

Une méthode universelle pour résoudre les problèmes LP est appelée la méthode du simplexe. Application de cette méthode et de sa modification la plus courante - la méthode du simplexe en deux phases.

Dans la méthode graphique de résolution des problèmes LP, on choisit en fait parmi l'ensemble des sommets appartenant à la limite de l'ensemble des solutions du système d'inégalités le sommet auquel la valeur de la fonction objectif atteint un maximum (minimum). Dans le cas de deux variables, cette méthode est totalement intuitive et permet de trouver rapidement une solution au problème.

Si un problème comporte trois variables ou plus, et que c'est exactement le cas dans les problèmes économiques réels, il est difficile de visualiser la zone de solution du système de contraintes. De tels problèmes sont résolus en utilisant méthode simplexe ou par la méthode des améliorations successives. L’idée de la méthode est simple et est la suivante.

Selon une certaine règle, le plan de référence initial (un sommet de la zone de contrainte) est trouvé. Il vérifie si le plan est optimal. Si oui, alors le problème est résolu. Sinon, nous passons à un autre plan amélioré - à un autre sommet. la valeur de la fonction objectif sur ce plan (en ce sommet) est évidemment meilleure que dans le précédent. L'algorithme de transition est réalisé à l'aide d'une certaine étape de calcul, qui est commodément écrite sous forme de tableaux appelés tableaux simplexes . Puisqu’il existe un nombre fini de sommets, en un nombre fini d’étapes, nous arrivons à la solution optimale.

Considérons la méthode du simplexe à l'aide d'un exemple précis du problème de l'élaboration d'un plan.

Notons encore une fois que la méthode du simplexe est applicable à la résolution de problèmes canoniques LP réduits à une forme particulière, c'est-à-dire ayant une base, des membres droits positifs et une fonction objectif exprimée en termes de variables non fondamentales. Si la tâche n'est pas réduite à une forme particulière, des étapes supplémentaires sont nécessaires, dont nous parlerons plus tard.

Considérons le problème d'un plan de production, après avoir préalablement construit un modèle et l'avons amené à une forme particulière.

Tâche.

Pour la fabrication de produits UN Et DANS L'entrepôt ne peut pas libérer plus de 80 unités de matières premières. De plus, pour la fabrication du produit UN deux unités sont consommées, et les produits DANS- une unité de matières premières. Il est nécessaire de planifier la production de manière à assurer le plus grand profit si les produits UN il n'est pas nécessaire de produire plus de 50 pièces et des produits DANS- pas plus de 40 pièces. De plus, le bénéfice de la vente d'un produit UN- 5 roubles, et à partir de DANS- 3 frotter.

Construisons un modèle mathématique, désignant X 1 quantité de produits A en plan, pour X 2 - nombre de produits DANS. alors le système de contraintes ressemblera à ceci :

x1 ≤50
x2 ≤40
2x 1 +x 2 ≤80
x1 ≥0, x2 ≥0
5x 1 +3x 2 →maximum

Amenons le problème sous forme canonique en introduisant des variables supplémentaires :

x1 +x3 =50
x2 +x4 =40
2x 1 +x 2 +x 5 =80
x1 ≥0, x2 ≥0
5x 1 +3x 2 →maximum
-F = -5x 1 - 3x 2 → min.

Ce problème a une forme particulière (avec une base, les membres de droite sont non négatifs). Il peut être résolu en utilisant la méthode du simplexe.

jescène. Enregistrer un problème dans un tableau simplexe. Il existe une correspondance bijective entre le système de contraintes du problème (3.10) et la table simplexe. Il y a autant de lignes dans le tableau qu'il y a d'égalités dans le système de contraintes, et il y a autant de colonnes que de variables libres. Les variables de base remplissent la première colonne, les variables libres remplissent la ligne supérieure du tableau. La ligne du bas s'appelle la ligne d'index ; les coefficients des variables de la fonction objectif y sont écrits. Dans le coin inférieur droit, 0 est initialement écrit s'il n'y a pas de membre libre dans la fonction ; si c'est le cas, écrivez-le avec le signe opposé. A cet endroit (dans le coin inférieur droit) se trouvera une valeur de la fonction objectif, qui devrait augmenter en valeur absolue lors du passage d'un tableau à l'autre. Ainsi, le tableau 3.4 correspond à notre système de restrictions, et nous pouvons passer à l'étape II de la solution.

Tableau 3.4

basique			gratuit

IIscène. Vérification de l'optimalité du plan de référence.

Ce tableau 3.4 correspond au plan de référence suivant :

(X 1 , X 2 , X 3 , X 4 , X 5) = (0, 0, 50, 40, 80).

Variables libres X 1 , X 2 est égal à 0 ; X 1 = 0, X 2 = 0. Et les variables de base X 3 , X 4 , X 5 prendre des valeurs X 3 = 50, X 4 = 40, X 5 = 80 - dans la colonne des conditions gratuites. Valeur de la fonction objectif :

-F = - 5X 1 - 3X 2 = -5 0 - 3 0 = 0.

Notre tâche est de vérifier si un plan de référence donné est optimal. Pour ce faire, vous devez regarder la ligne d'index - la ligne de fonction cible F.

Diverses situations sont possibles.

1. Dans l'index F- il n'y a aucun élément négatif dans la chaîne. Cela signifie que le plan est optimal et qu’une solution au problème peut être écrite. La fonction objectif a atteint sa valeur optimale, égale au nombre en bas à droite, pris avec le signe opposé. Passons à l'étape IV.

2. La ligne d'index contient au moins un élément négatif dont la colonne ne contient aucun élément positif. Nous concluons alors que la fonction objectif F→∞ diminue sans limite.

3. La ligne d'index comporte un élément négatif qui possède au moins un élément positif dans sa colonne. On passe ensuite à l'étape III suivante. Nous recalculons le tableau, améliorant le plan de référence.

IIIscène. Amélioration du plan de référence.

Des éléments négatifs de l'indice F-lignes, sélectionnez celle avec le module le plus grand, appelez la résolution de colonne correspondante et marquez-la avec « ».

Pour sélectionner une ligne résolvante, il faut calculer les ratios des éléments de la colonne des termes libres seulementÀ positiféléments de la colonne de résolution. Sélectionnez la relation minimale parmi les relations obtenues. L'élément correspondant auquel le minimum est atteint est appelé résolution. Nous le soulignerons avec un carré.

Dans notre exemple, l'élément 2 est permissif. La droite correspondant à cet élément est aussi appelée résolution (tableau 3.5).

Tableau 3.5

Après avoir sélectionné l'élément permettant, nous recalculons le tableau selon les règles :

1. Dans un nouveau tableau de même taille que précédemment, les variables de la ligne et de la colonne de résolution sont permutées, ce qui correspond au passage à une nouvelle base. Dans notre exemple : X 1 est inclus dans la base, à la place X 5, qui quitte la base et est désormais libre (tableau 3.6).

Tableau 3.6

2. À la place de l'élément résolvant 2, écrivez son nombre inverse ½.

3. Nous divisons les éléments de la ligne de résolution par l'élément de résolution.

4. Nous divisons les éléments de la colonne de résolution par l'élément de résolution et les écrivons avec le signe opposé.

5. Pour remplir les éléments restants du tableau 3.6, nous recalculons en utilisant la règle du rectangle. Disons que nous voulons compter l'élément en position 50.

Nous connectons mentalement cet élément avec celui de résolution, trouvons le produit, soustrayons le produit des éléments situés sur l'autre diagonale du rectangle résultant. Nous divisons la différence par l'élément résolvant.

Donc, . On écrit 10 à la place où il y en avait 50. De même :
, , , .

Tableau 3.7

Nous avons un nouveau tableau 3.7, les variables de base sont désormais les variables (x 3,x 4,x 1). La valeur de la fonction objectif est devenue -200, c'est-à-dire diminué. Pour vérifier l’optimalité de cette solution de base, il faut revenir à l’étape II. Le processus est évidemment fini, le critère d'arrêt étant les points 1 et 2 de l'étape II.

Terminons la solution du problème. Pour ce faire, vérifions la ligne d'index et, y voyant un élément négatif -½, appelons la résolution de colonne correspondante et, selon l'étape III, recalculons le tableau. Après avoir compilé les relations et choisi parmi elles le minimum = 40, nous avons déterminé l'élément de résolution 1. Nous effectuons maintenant le recalcul selon les règles 2 à 5.

Tableau 3.8

Après avoir recalculé le tableau, nous nous assurons qu'il n'y a pas d'éléments négatifs dans la ligne d'index. Le problème est donc résolu, le plan de base est optimal.

IVscène. Écrire la solution optimale.

Si la méthode simplexe s'est arrêtée selon le point 1 de l'étape II, alors la solution au problème s'écrit comme suit. Les variables de base prennent en conséquence les valeurs de la colonne des termes factices. Dans notre exemple X 3 = 30, X 2 = 40, X 1 = 20. Les variables libres sont 0, X 5 = 0, X 4 = 0. La fonction objectif prend la valeur du dernier élément de la colonne des termes libres de signe opposé : - F = -220 → F= 220, dans notre exemple la fonction a été examinée au min, et initialement F→ max, donc le signe a en fait changé deux fois. Donc, X* = (20, 40, 30, 0, 0), F* = 220. Réponse au problème :

Il est nécessaire d'inclure 20 produits du type dans le plan de production UN, 40 produits de type B, tandis que le bénéfice sera maximum et sera égal à 220 roubles.

À la fin de cette section, nous présentons un organigramme de l'algorithme de la méthode simplex, qui répète exactement les étapes, mais peut-être pour certains lecteurs, il sera plus pratique à utiliser, car les flèches indiquent une direction claire des actions.

Les liens au-dessus des cases de l'organigramme indiquent à quelle étape ou sous-point appartient le groupe de transformations correspondant. la règle de recherche du plan de référence initial sera formulée au paragraphe 3.7.

Exemple. Résolvez le problème LP suivant sous forme canonique en utilisant la méthode du simplexe.
f(x)=x 1 +9x 2 +5x 3 +3x 4 +4x 5 +14x 6 → min
x1 +x4 =20
x2 +x5 =50
x3 +x6 =30
x4 +x5 +x6 =60
x je ≥ 0, je = 1,…,6
Un problème LP est dit avoir une forme canonique si toutes les restrictions (à l'exception des conditions de non-négativité des variables) ont la forme d'égalités et si tous les termes libres sont non négatifs. Nous avons donc le problème sous forme canonique.
L'idée de la méthode simplexe est la suivante. Vous devez d’abord trouver un sommet (initial) du polyèdre des solutions réalisables (solution de base réalisable initiale). Ensuite, vous devez vérifier l'optimalité de cette solution. Si c’est optimal, alors une solution a été trouvée ; sinon, allez à un autre sommet du polyèdre et vérifiez à nouveau l'optimalité. En raison de la finitude des sommets du polyèdre (conséquence de la finitude des contraintes du problème LP), en un nombre fini de « pas » nous trouverons le point minimum ou maximum requis. Il est à noter que lors du passage d'un sommet à un autre, la valeur de la fonction objectif diminue (dans le problème minimum) ou augmente (dans le problème maximum).
Ainsi, l'idée de la méthode simplex repose sur trois propriétés du problème LP.
Solution. Pour trouver la solution de base réalisable initiale, c'est-à-dire pour déterminer les variables de base, le système (5.6) doit être réduit à une forme « diagonale ». En utilisant la méthode gaussienne (méthode d’élimination séquentielle des inconnues), on obtient de (5.6) :
x2 +x1 +x3 =40
x4 +x1 =20
x 5 -x 1 -x 3 =10
x6 +x3 =30
Les variables de base sont donc x2 , x4 , x5 , x6 , On leur donne des valeurs égales aux membres libres des chaînes correspondantes : x2 =40, x4 =20, x5 =10, x6 =30,. Variables x1 Et x3 ne sont pas basiques : x1 =0, x3 =0.
Construisons la solution de base réalisable initiale
x 0 = (0,40,0,20,10,30) (5,9)
Pour vérifier l'optimalité de la solution trouvée x0 il est nécessaire d'exclure les variables de base de la fonction cible (en utilisant le système (5.8)) et de construire une table simplex spéciale.
Après avoir éliminé les variables, il convient d'écrire la fonction objectif sous la forme :
f(x) = -7x 1 – 14x 3 +880 (5.10)
Maintenant, en utilisant (5.8)–(5.10), nous composons le tableau simplex initial :

La ligne zéro contient les coefficients de signe opposé des variables correspondantes pour la fonction objectif. Critère d'optimalité (pour le problème de recherche minimum) : solution de base admissible ( x0) est optimal s'il n'y a pas un seul nombre strictement positif dans la ligne zéro (sans compter la valeur de la fonction objectif (880)). Cette règle s'applique également aux itérations ultérieures (tableaux). Les éléments de la ligne zéro seront appelés estimations de colonnes.
Ainsi, la solution de base réalisable initiale (5.9) est sous-optimale : 7>0, 14>0 .
La colonne zéro contient les valeurs des variables de base. Ils doivent être non négatifs (voir équation (5.7)). Les coefficients des variables du système (5.8) sont écrits de la première à la quatrième ligne.
Parce que x0 n'est pas optimal, alors il faut passer à un autre sommet du polyèdre des solutions admissibles (construire un nouveau d.b.r.). Pour ce faire, vous devez trouver l'élément leader et effectuer une certaine transformation (transformation simplex).
Tout d'abord, nous trouvons l'élément de tête du tableau, qui se situe à l'intersection de la colonne de tête (la colonne avec le score positif le plus élevé) et de la ligne de tête (la ligne correspondant au rapport minimum des éléments de la colonne zéro sur le éléments correspondants (strictement positifs) de la première colonne).
Dans le tableau 1, la première colonne est la troisième colonne et la première ligne est la quatrième ligne. (min(40/1,30/1)=30/1) sont indiqués par des flèches et l'élément principal est indiqué par un cercle. L'élément principal indique que la variable sous-jacente x6 doit être remplacé par un modèle non basique x3. Alors les nouvelles variables de base seront x2 , x3 , x4 , x5 ,, et non basique - x1, x6,. Cela signifie la transition vers un nouveau sommet du polyèdre des solutions admissibles. Pour trouver les valeurs de coordonnées d'une nouvelle solution de base réalisable x00 vous devez construire une nouvelle table simplexe et y effectuer des transformations élémentaires :
UN) divisez tous les éléments de la ligne directrice par l'élément principal, transformant ainsi l'élément principal en 1 (pour faciliter le calcul) ;
b) en utilisant l'élément de début (égal à 1), transformez tous les éléments de la colonne de début en zéros (similaire à la méthode d'élimination des inconnues) ;
En conséquence, les valeurs des nouvelles variables de base sont obtenues dans la colonne zéro x2 , x3 , x4 , x5 ,(voir tableau 2) - composants de base du nouveau sommet x00(composants non basiques x1 =0, x6 =0,).

Comme le montre le tableau 2, la nouvelle solution de base x00 =(0,10,30,20,40,0) sous-optimal (la ligne zéro contient un score non négatif de 7). Par conséquent, avec l'élément principal 1 (voir tableau 2), nous construisons une nouvelle table simplexe, c'est-à-dire construire une nouvelle solution de base réalisable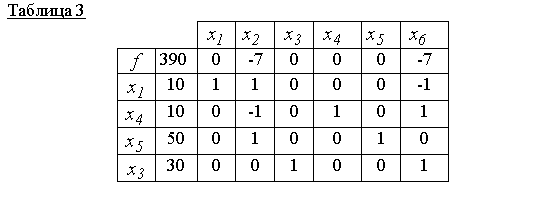

Le tableau 3 correspond à une solution de base acceptable x 000 =(10,0,30,10,50,0) et c'est optimal, car il n'y a pas de notes positives dans la ligne zéro. C'est pourquoi f(x 000)=390 est la valeur minimale de la fonction objectif.
Répondre: x 000 =(10, 0, 30, 10, 50, 0)- point minimum, f(x 000)=390.

Problème de programmation linéaire classiquement standard

Vous devez effectuer les tâches suivantes dans l'ordre indiqué.

1. Trouvez le plan optimal pour le problème direct :
   a) méthode graphique ;
   b) en utilisant la méthode du simplexe (pour construire le plan de référence initial, il est recommandé d'utiliser la méthode des bases artificielles).
2. Construisez un double problème.
3. Trouver le plan optimal pour le problème dual à partir de la solution graphique de la droite, en utilisant les conditions de relâchement complémentaire.
4. Trouvez le plan optimal pour le problème dual en utilisant le premier théorème de dualité, en utilisant la table simplexe finale obtenue en résolvant le problème direct (voir section 1b). Vérifiez l'énoncé « les valeurs des fonctions objectives d'une paire de problèmes duaux coïncident dans leurs solutions optimales ».
5. Résolvez le problème dual en utilisant la méthode du simplexe, puis, en utilisant la table simplexe finale du problème dual, trouvez le plan optimal pour le problème direct en utilisant le premier théorème de dualité. Comparez le résultat avec le résultat obtenu graphiquement (voir paragraphe 1a).
6. Trouvez la solution entière optimale :
   a) méthode graphique ;
   b) Méthode Gomori.
   Comparez les valeurs des fonctions de solution entières et non entières

Questions pour la maîtrise de soi

1. Comment est construite une table simplexe ?
2. Comment un changement de base est-il reflété dans le tableau ?
3. Formulez un critère d'arrêt pour la méthode simplexe.
4. Comment organiser le recalcul des tables ?
5. Quelle ligne est pratique pour commencer à recalculer le tableau ?

Si dans le problème que nous venons d'examiner, la première solution fondamentale obtenue s'avère admissible, alors dans d'autres cas, elle peut être trouvée non pas immédiatement, mais après un certain nombre d'étapes.

Il faut se rappeler qu'à la première étape de la méthode du simplexe, c'est-à-dire lors de la recherche d'une solution réalisable, la forme linéaire n'est pas prise en compte et toutes les transformations concernent uniquement le système de contraintes.

Soit le problème de programmation linéaire sous forme générale, c'est-à-dire système de m équations linéaires à n variables (m

Par conséquent, cette méthode de division des variables en variables basiques et non basiques correspond à la solution de base... ; 0 ; 0;…;0.

Considérons le cas général où cette solution est inacceptable. De la solution basique obtenue, il faut d'abord passer à une solution basique admissible, et il n'est pas nécessaire que cette transition soit effectuée immédiatement, en une seule étape.

Si le système de contraintes n'est pas incohérent, alors après un nombre fini d'étapes, la transition vers une solution de base admissible sera effectuée.

Par hypothèse, la solution de base originale n’est pas valide. Par conséquent, parmi les membres libres du système de contraintes, il y en a au moins un négatif (le nombre de membres libres négatifs de ce système coïncide avec le nombre de composantes négatives de la solution de base originale). Que ce soit un membre gratuit ok jeéquations i-ro, c'est-à-dire la variable principale x je dans la solution basique correspondante est négatif.

Pour passer à une nouvelle solution de base, deux problèmes doivent être résolus :

1) établir quelle variable non fondamentale doit être convertie en variable principale ;

2) sélectionner une variable qui doit être transférée des variables principales vers les variables non basiques à la place de celle qui a été supprimée des variables principales.

Lors de la conversion d'une variable non fondamentale en variable majeure, elle ne diminue pas, mais, en règle générale, augmente : au lieu de zéro dans la solution de base d'origine, elle prendra une valeur positive dans la nouvelle solution de base (une exception se produit uniquement en cas de dégénérescence). Par conséquent, pour résoudre la question de savoir quelles variables non fondamentales peuvent être converties en variables de base, vous devez être capable de trouver des variables non fondamentales, avec une augmentation dans laquelle la variable principale, négative dans la solution de base originale, augmente. Revenons à la i-ième équation du système, dans laquelle le terme libre ok je négatif. Cela montre que la variable x je augmente avec l'augmentation des variables non fondamentales dont les coefficients dans cette équation sont positifs. Il s'ensuit que les variables non fondamentales qui ont des coefficients positifs dans l'équation d'un système avec un terme libre négatif peuvent être converties en variables de base.

Trois cas peuvent se présenter ici.

1. Dans la ième équation du système, il n'y a pas de variables mineures avec des coefficients positifs, c'est-à-dire tous les coefficients b je, j sont négatifs (tout comme le terme libre ki). Dans ce cas, ce système de restrictions est incohérent : il n’existe pas une seule solution admissible. En effet, du fait de la non-négativité de toutes les variables, y compris x m + l ,...,x n , la i-ième équation dans laquelle le terme libre ok je et tous les coefficients b je , m + l ,...,b je , n sont négatifs, il s'ensuit que la variable x je- ne peut pas prendre de valeurs non négatives. Mais s’il n’existe pas une seule solution réalisable à un système de contraintes, alors il n’y a pas de solution optimale.

2. La i-ième équation a une variable x t + j, dont le coefficient est positif. Dans ce cas, c'est cette variable qui est transférée aux principales.

3. La i-ème équation comporte plusieurs variables avec des coefficients positifs. Dans ce cas, n'importe lequel d'entre eux peut être converti en base.

Ensuite, vous devez déterminer quelle variable principale doit être convertie en variable non basique. Pour ce faire, vous devez utiliser la règle : trouver les rapports des termes libres aux coefficients de la variable convertie en principaux à partir de toutes les équations où les signes des termes libres et les coefficients indiqués sont opposés, puis considérer le valeur absolue de ces rapports et sélectionnez le plus petit parmi eux (si dans certaines équations les signes termes libres et coefficients coïncident ou dans certaines équations il n'y a pas de variable pouvant être convertie en variables de base, alors le rapport est considéré comme égal à ∞).

L'équation à partir de laquelle le plus petit rapport est obtenu est isolée. L'équation en surbrillance montre laquelle des variables principales doit être convertie en variables non fondamentales. Après avoir exprimé les nouvelles variables principales en termes de variables non fondamentales, ils passent à la solution fondamentale suivante.

Le résultat est un système d'équations similaire au système, dans lequel le nombre d'érables libres négatifs coïncide avec leur nombre dans le système ou est inférieur d'un. Cela dépend si l'ordonnée à l'origine dans l'équation en surbrillance est positive ou négative.

Si le terme libre dans l'équation sélectionnée est négatif, alors dans la nouvelle solution de base, le nombre de composants négatifs sera inférieur d'un à celui de la solution d'origine. Si dans l'équation sélectionnée le terme libre est positif (ou égal à zéro), alors dans la nouvelle solution de base, le nombre de composantes négatives restera le même que dans la solution d'origine.

Nous obtenons ainsi une nouvelle solution de base améliorée, plus proche de la région des solutions réalisables au système de contraintes. Si cela s’avère inacceptable, le même schéma devrait alors être appliqué à nouveau. En conséquence, après un nombre fini d’étapes, une solution basique admissible sera obtenue.

Suite de l'exemple 4.1. Nous devons trouver une solution de base admissible à ce système de contraintes qui maximiserait la forme linéaire.

Étant donné que le système de contraintes est un système de quatre équations indépendantes à six variables, le nombre de variables principales doit être de quatre et le nombre de variables non fondamentales doit être de deux.

Pour résoudre un problème à l’aide de la méthode simplexe, vous devez tout d’abord trouver une solution de base. Dans ce cas, c'est facile à faire. Pour ce faire, il suffit de prendre des variables supplémentaires comme principales X 3 , X 4 , X 5 , X 6. Puisque les coefficients de ces variables forment une matrice d’identité, il n’est pas nécessaire de calculer le déterminant. Comptage des variables non essentielles X 1 , X 2 égal à zéro, on obtient la solution de base (0 ; 0 ; 120 ; 160 ; 120 ; 80), qui s'est également avérée admissible. Il n’est donc pas nécessaire d’appliquer la première étape de la méthode du simplexe.

On passe directement à la deuxième étape, c'est à dire à la recherche d'une solution optimale.

1 étape. Variables principales : x 3, x 4, x 5, x 6 ; variables non essentielles : X 1 , X 2. Dans le système, nous exprimons les principales variables par des variables non fondamentales. Afin de juger s'il faut laisser les variables non fondamentales parmi les variables non fondamentales ou s'il est plus rentable du point de vue de l'approche de la solution optimale de les transférer aux principales, il est nécessaire d'exprimer une forme linéaire par eux (dans ce cas, il est déjà exprimé à travers les variables X 1 , X 2) On obtient alors :

À X 1 = X 2 = 0 nous avons X 3 = 120, X 4 = 160, X 5 = 120, X 6 = 80, ce qui donne la solution de base (0 ; 0 ; 120 ; 160 ; 120 ; 80), que nous avons prise comme solution initiale. Avec cette solution de base, la valeur de la forme linéaire =0.

Quand nous pensions X 1 = X 2 = 0 (la production ne produit rien), l'objectif était fixé : trouver la première solution de base, quoi qu'il arrive. Cet objectif a été atteint. Il faut maintenant passer de cette solution initiale à une autre, dans laquelle la valeur de la forme linéaire va augmenter. De la considération de la forme linéaire, il est clair que sa valeur augmente avec l'augmentation des valeurs des variables X 1 et X 2. En d'autres termes, il n'est pas rentable de considérer ces variables comme non fondamentales, c'est-à-dire égales à zéro, il faut les convertir en nombre de principales. Cela signifie une transition vers une nouvelle solution de base. Avec la méthode du simplexe, à chaque étape de la solution, on suppose qu'une seule des variables libres est convertie en la variable principale. Convertissons la variable en nombre de variables de base X 2, puisqu'elle est incluse dans l'expression de la forme linéaire à grand coefficient.

Dès qu'une des variables libres devient l'une des principales, l'une des principales doit être transférée à sa place au nombre de variables non fondamentales. Laquelle des quatre variables principales faut-il déduire ? Les considérations suivantes aideront à répondre à cette question.

Signification X 2 doit être rendu aussi grand que possible, car cela correspond à l'objectif final - la maximisation F. Il s’avère cependant que l’augmentation X 2 ne peut continuer que jusqu'à des limites connues, c'est-à-dire jusqu'à ce que l'exigence de non-négativité des variables soit violée. Ainsi, de la première équation du système, il s'ensuit que la variable x 2 ne doit pas dépasser le nombre 120/4, c'est-à-dire X 2 ≤30, car seulement avec ces valeurs X 2 variables X 3 reste positif (si X 2 = 30, alors X 3 = 0 ; si X 2 > 30, puis X 3 < 0). Из третьего уравнения системы следует, что X 2 ≤ 120/2, soit X 2 ≤ 60, à partir du quatrième - quoi X 2 ≤ 80/2, soit X 2 ≤ 40 (dans la deuxième équation la variable X 2 non inclus). Remplit toutes ces conditions X 2 ≤ 30.

En d'autres termes, pour répondre à la question de savoir quelle variable doit être convertie en variable non basique, vous devez accepter X 2 = min (120/4 ; 120/2 ; 80/2) = min (30 ; 60 ; 40) = 30. Alors X 3 = 0 et X 3 devient une variable non primaire, et x 4 et x 5 restent positifs,

Étape 2. Variables clés : X 2 , X 4 , X 5 , X 6 variables mineures : X 1 et X 3. Exprimons les principales variables et la forme linéaire en termes de variables non fondamentales. Dans le système on prend l'équation à partir de laquelle la valeur minimale du rapport du terme libre au coefficient à X 2. Dans ce cas, c'est la première équation. Exprimer à partir de cette équation X 2, nous avons, X 2 = 30 - 0,25 · X 3. Remplaçons cette expression X 2 dans toutes les autres équations du système (4.4) et sous forme linéaire F et, en ramenant des termes similaires, nous obtenons

À X 1 = X 3 = 0 nous avons F= 90. C'est déjà mieux qu'à l'étape 1, mais pas le maximum souhaité. Augmentation supplémentaire de la fonction F possible en introduisant une variable X 1 parmi les principaux ; puisque cette variable est incluse dans l'expression F avec un coefficient positif, donc son augmentation entraîne une augmentation sous la forme linéaire et il n'est pas rentable de la considérer comme non basique, c'est-à-dire égal à zéro.

Pour répondre à la question de savoir quelle variable déduire des principales aux non fondamentales, on accepte X 1 = min (160/4 ; 60/2 ; 20/1) = 20. Alors X 6 = 0 et X 6 devient une variable non principale, et X 4 et X 5 restent positifs.

La première équation n'est pas utilisée pour trouver le minimum spécifié, car X] n’est pas inclus dans cette équation.

Étape 3. Variables clés : X 1 , x2 , x4 , x5 ; variables mineures : x 3, x 6. Exprimons les principales variables et la forme linéaire en termes de variables non fondamentales. A partir de la dernière équation du système (4.5) (elle est mise en évidence) on a X 1 = 20 + 0,5 · X 3 - X 6. En substituant cette expression dans les équations restantes et sous forme linéaire, nous obtenons

De l'expression de la forme linéaire, il résulte que sa valeur maximale n'a pas encore été obtenue, puisqu'une augmentation est possible F en introduisant dans la variable principale X 3 (il a un coefficient positif). Nous croyons X 3 = min (∞ ; 30/0,25 ; 80/2 ; 20/0,5) =40.

Ici, nous rencontrons d’abord deux dispositions qui nécessitent des précisions supplémentaires.

Premièrement, même si la variable X 3 et est inclus dans l’expression de X 1 (la première équation du système (4.6), mais a un coefficient positif pour toute augmentation X 3 variables X 1 ne peut pas devenir négatif. En d’autres termes, dans la première équation, il n’y a aucune restriction sur l’augmentation de la variable X 3 ne se chevauche pas, on écrit donc classiquement ∞. À l'avenir, nous accepterons d'utiliser la même notation si la variable, nouvellement introduite dans la liste des variables fondamentales, n'est incluse dans aucune équation du système de contraintes.

Deuxièmement, nous obtiendrons deux valeurs minimales identiques égales à 40. Si X 3 = 40, alors X 4 = 0 et x5 = 0, c'est-à-dire la conclusion suggère qu'au lieu d'une variable, deux devraient être transférées au nombre de non basiques à la fois : X 4 et x5. Mais le nombre de variables principales ne doit pas être inférieur à quatre. Pour ce faire, procédez comme suit. Une des variables ( X 4 ou X 5.) est laissé parmi les solutions basiques, mais sa valeur est considérée comme égale à zéro, c'est-à-dire que la solution basique obtenue à l'étape suivante s'avère dégénérée. Laissons, par exemple, X 4 parmi les principales variables, et X 5 seront transférés au nombre de non-essentiels.

Étape 4 Variables clés : X 1, x 2, X 3 , X 4 ; variables non principales : x 5, x 6. Exprimons les principales variables et forme linéaire F en passant par les non primaires, en commençant cette expression à partir de la quatrième équation du système (4.6). En conséquence nous obtenons

Puisque dans l'expression d'une forme linéaire les variables X 5 et X 6 entrez avec des coefficients négatifs, puis pas d'augmentation F en raison de ces variables est impossible.

L'absence à une étape quelconque de la méthode du simplexe dans l'expression de la forme linéaire F, dont le maximum est recherché, de variables mineures à coefficients positifs est un critère d'optimalité.

Par conséquent, à l’étape 4, le critère d’optimalité est atteint et le problème est résolu. La solution optimale est (40 ; 20 ; 40 ; 0 ; 0 ; 0), dans laquelle F maximum =140. Ainsi, pour obtenir le plus grand profit égal à 140 deniers. unités, à partir de ces ressources, il faut obtenir 40 unités de production à partir de champs de foin et 20 à partir de terres arables. Dans ce cas, les ressources des types II, III et IV seront entièrement utilisées, soit 40 unités. Tapez Je ne serai pas dépensé.

Exemple 4.2. Trouver le maximum d'une fonction F=x 1 + 2 X 2 avec restrictions

Nous introduisons des variables supplémentaires non négatives X 3 ,X 4 ,X 5 ,X 6 et réduire ce système d’inégalités à son système d’équations équivalent

Nous prenons les variables supplémentaires introduites comme principales, car dans ce cas, la solution de base du système est facile à trouver. Alors X 1 et X 2 - variables mineures.

1 étape. Variables clés : X 3 ,X 4 , X 5 , X 6 ; variables non essentielles ; X 1 et X 2. En exprimant les principales variables en termes de variables non fondamentales, nous obtenons

Par conséquent, cette division des variables en basiques et non basiques correspond à la solution de base (0 ; 0 ; - 2 ; - 4 ; 2 ; 6), ce qui est inacceptable (deux variables sont négatives), et donc elle n'est pas optimale. De cette solution de base, nous passerons à une solution améliorée.

Pour décider quelle variable doit être transférée du mineur au fondamental, considérons l'une des deux équations disponibles de ce dernier système à termes libres négatifs, par exemple la seconde. Cela montre qu'il est possible de traduire en variables de base X 1 et X 2, puisque dans cette équation ils ont des coefficients positifs (d'où, lorsqu'ils augmentent, que se passera-t-il si l'on traduit l'un d'entre eux en variables principales, la variable X 4 augmentera).

Essayons de le traduire dans la variable principale X 1 . Pour établir quelle variable doit être transférée du basique au non basique, on trouve la valeur absolue du plus petit rapport des termes libres du système aux coefficients à X 1 , nous avons X 1 = min (∞ ; 4/1 ; 2/1 ; ∞) = 2. Il est obtenu à partir de la troisième équation, montrant que la variable doit être convertie en variables mineures X 5, ce qui est positif dans la solution de base originale.

Par conséquent, la solution de base résultante, comme celle d'origine, contient deux composants négatifs, c'est-à-dire qu'en passant à une telle solution de base, il n'y aura aucune amélioration.

Si on traduit dans la variable principale X 2 , alors le plus petit rapport termes libres/coefficients à X 2 sera X 2 - min (2/2 ; 4/1 ; ∞ ; 6/1) = 1. Il est obtenu à partir de la première équation, dans laquelle le terme libre est négatif. Par conséquent, traduire X 2 dans les principaux, et X 3 en variables mineures, nous obtenons une solution de base dans laquelle le nombre de composantes négatives est inférieur d'une à celle d'origine. Concentrons-nous donc sur cette possibilité : nous traduisons X 2 dans les principaux, et X 3 en variables non principales ; alors la première équation sera mise en évidence.

Étape 2. Variables clés : X 2 ,X 4 ,X 5 ,X 6 ; variables non essentielles : X 1 et X 3. Exprimons les nouvelles variables principales à travers les nouvelles variables non fondamentales, en commençant par l'équation mise en évidence à l'étape 1. En conséquence nous obtenons

Par conséquent, nous avons une nouvelle solution de base (0 ; 1 ; 0 ; -3 ; 3 ; 5), qui est également invalide et donc non optimale. Mais, comme nous l'avions prédit, une seule variable est négative (à savoir X 4).

De la solution de base obtenue, il faut passer à une autre. Considérons une équation avec un terme libre négatif, c'est-à-dire deuxième équation. Cela montre qu'il est possible de traduire en variables de base X 1 et X 3. Convertissons en variables principales X 1 . Trouvons la plus petite des valeurs absolues des rapports des termes libres du système aux coefficients à X 1 ; nous avons X 1 = min (∞ ; 3/1,5 ; 3/0,5 ; 5/0,5) = 2. Cela signifie que nous devons convertir X 4 . Puisque le plus petit rapport est obtenu à partir de la deuxième équation, nous l’isolons. La nouvelle solution de base ne contiendra plus de composants négatifs, c'est-à-dire qu'elle est admissible.

Étape 3. Variables clés : X 1 , X 2 , X 5 , X 6 ; variables non essentielles : X 3 , X 4 . En exprimant les principales variables en termes de variables non fondamentales, nous obtenons

La nouvelle solution de base a la forme (2 ; 2 ; 0 ; 0 ; 2 ; 4). On peut déterminer si elle est optimale en exprimant une forme linéaire en termes de variables mineures de la solution de base considérée. Ceci fait, nous obtenons . Ainsi, nous recourons à la forme linéaire uniquement lorsque la solution de base est réalisable. Puisque nous recherchons le maximum d’une forme linéaire, la solution de base résultante n’est pas optimale.

Conversion du nombre de variables principales X 4 ayant un coefficient positif plus grand.

Nous trouvons X 4 = min (∞ ; ∞ ; 2 : (1/3) ; 4/(1/3)) = 6. Ce plus petit rapport est obtenu à partir de la troisième équation du système, que nous sélectionnons. Cela montre que lorsque X 4 =6 variable X 5 = 0 et deviendra donc non primaire.

Étape 4 Variables clés : X 1 , X 2 , X 4 , X 6;variables mineures : X 3 , X 5 . En exprimant les principales variables en termes de variables non fondamentales, nous obtenons

La forme linéaire, exprimée à travers les mêmes variables non fondamentales, prendra la forme . Par conséquent, la solution de base (6 ; 4 ; 0 ; 6 ; 0 ; 2) vers laquelle nous sommes passés n’est pas optimale.

Une augmentation de la forme linéaire est possible lors du passage à une nouvelle solution de base, dans laquelle la variable x 3 est la principale. Nous trouvons X 3 = min (∞; ∞; co; 2/1) = 2. Ce plus petit rapport est obtenu à partir de la quatrième équation du système et montre que lorsque X 3 = 2 variables X 6 = 0 et devient non primaire.

Étape 5 Variables clés : X 1 , X 2 , X 3 , X 4 variables mineures X 5 ,X 6. En exprimant les principales variables en termes de variables non fondamentales, nous obtenons

La forme linéaire, exprimée en termes de variables mineures de la nouvelle solution de base, a la forme . Le critère d'optimalité pour le cas de maximisation de forme linéaire est satisfait. Par conséquent, la solution de base (8 ; 6 ; 2 ; 10, 0 ; 0) est optimale, et le maximum de la forme linéaire F maximum = 20.

4.5 Résolution de problèmes graphiques

programmation linéaire

Il est conseillé d'utiliser une méthode graphique pour résoudre des problèmes de programmation linéaire pour :

Solutions aux problèmes à deux variables lorsque les contraintes sont exprimées par des inégalités ;

Solutions aux problèmes avec de nombreuses variables, à condition que leur notation canonique ne contienne pas plus de deux variables libres.

Écrivons un problème de programmation linéaire avec deux variables :

fonction objectif :

restrictions :

Chacune des inégalités (4.8) du système de contraintes du problème définit respectivement géométriquement un demi-plan avec des droites frontières ; . Si le système d'inégalités (4.8) est cohérent, le domaine de ses solutions est l'ensemble des points appartenant à tous les demi-plans indiqués. Puisque l’ensemble des points d’intersection de ces demi-plans est convexe, la région des solutions réalisables est un ensemble convexe, appelé polygone de solution. Les côtés de ce polygone reposent sur des droites dont les équations sont obtenues à partir du système de contraintes original en remplaçant les signes d'inégalité par des signes d'égalité.

La région des solutions admissibles du système d'inégalités (4.8) peut être :

Polygone convexe ;

Zone polygonale convexe non délimitée ;

Zone vide ;

Segment de ligne;

Le seul point.

La fonction objectif (4.7) définit une famille de lignes parallèles sur le plan dont chacune correspond à une certaine valeur Z.

Un vecteur de coordonnées et , perpendiculaire à ces lignes, indique la direction de l'augmentation la plus rapide de Z, et le vecteur opposé indique la direction de diminution de Z.

Si l'on représente la région des solutions admissibles du système d'inégalités (4.8) et la famille des droites parallèles (4.7) dans le même système de coordonnées, alors le problème de la détermination du maximum de la fonction Z se réduira à trouver dans le admissible région le point par lequel passe une droite de la famille Z = const, et qui correspond à la plus grande valeur du paramètre Z.

Ce point existe lorsque le polygone de solution n'est pas vide et que la fonction objectif sur celui-ci est délimitée par le haut. Dans les conditions spécifiées, à l'un des sommets du polygone de solution, la fonction objectif prend la valeur maximale.

Pour déterminer ce sommet, nous construirons une ligne de niveau passant par l'origine des coordonnées et perpendiculaire au vecteur, et nous la déplacerons dans la direction du vecteur jusqu'à ce qu'elle touche le dernier point extrême (coin) du polygone de solution. Les coordonnées du point spécifié déterminent le plan optimal pour cette tâche.

Figure 4.1 - L'optimum de la fonction Z est réalisable au point A

Figure 4.2 - La fonction optimale Z est atteinte en tout point [AB]

En conclusion de notre examen de l'interprétation géométrique du problème (4.7) - (4.8), nous notons que lors de la recherche de sa solution, les cas illustrés à la Fig. 4.1 - 4.4. La figure 4.1 caractérise le cas où la fonction cible prend sa valeur maximale en un seul point A. D'après la figure 4.2, il ressort clairement que la fonction cible prend sa valeur maximale en tout point du segment AB.

Figure 4.3 - La fonction optimale Z est inaccessible

Figure 4.4 - Zone de solutions réalisables - zone vide

La figure 4.3 montre le cas où le maximum est inaccessible, et la figure 4.4 montre le cas où le système de contraintes du problème est incohérent. Notez que trouver la valeur minimale de Z sous un système de restrictions donné diffère de trouver sa valeur maximale sous les mêmes restrictions uniquement en ce que la ligne de niveau Z ne se déplace pas dans la direction du vecteur, mais dans la direction opposée. Ainsi, les cas mentionnés ci-dessus qui se produisent lors de la recherche de la valeur maximale de la fonction objectif se produisent également lors de la détermination de sa valeur minimale.

Pour résoudre pratiquement le problème de programmation linéaire (4.7) - (4.8) sur la base de son interprétation géométrique, ce qui suit est nécessaire.

1. Construire des droites dont les équations sont obtenues en remplaçant les signes d'inégalité dans les restrictions (4.4) par des signes égaux.

2. Trouver les demi-plans définis par chacune des contraintes du problème.

3.Définissez le polygone de solution.

4. Construisez un vecteur.

5.Construisez une ligne droite passant par l’origine des coordonnées et perpendiculaire au vecteur.

6. Déplacez la ligne droite dans la direction du vecteur , à la suite de quoi ils trouvent soit le (les) point(s) auquel la fonction objectif prend la valeur maximale, soit établissent le caractère illimité de la fonction d'en haut sur l'ensemble des plans .

7. Déterminez les coordonnées du point maximum de la fonction et calculez la valeur de la fonction objectif en ce point.

Exemple 4.3. L'entreprise fabrique deux types de produits P et R, vendus en gros. Pour la production de produits, on utilise deux types de matières premières A et B. Les approvisionnements maximum possibles en matières premières par jour seront respectivement de 9 et 13 unités. La consommation de matières premières de type A pour la fabrication des produits P et P sera respectivement de 2 et 3 unités de type B - 3 et 2 unités. L'expérience a montré que la demande quotidienne du produit P ne dépasse jamais la demande du produit P de plus d'une unité. De plus, on sait que la demande en produit P ne dépasse jamais 2 unités par jour. Les prix de gros par unité de production sont égaux à 3 unités pour P et 4 unités pour P. Quelle quantité de chaque type de produit l'entreprise doit-elle produire pour maximiser les revenus des ventes. Résolvez le problème en utilisant une méthode géométrique.

Solution. Construisons un polygone de solutions (Fig. 7.5). Pour ce faire, dans le repère X 1 OX 2 sur le plan, on trace les lignes limites :

En prenant n'importe quel point, par exemple l'origine, on détermine quel demi-plan définit l'inégalité correspondante. Demi-plans définis par les inégalités de la Fig. 7.5 sont représentés par des flèches. Le domaine de solution est le polygone OABCD.

Pour construire une ligne droite, nous construisons un vecteur gradient et passant par le point 0 nous traçons une ligne droite perpendiculaire à celui-ci. On déplace la droite construite Z= 0 parallèlement à elle-même dans la direction du vecteur. De la figure 4.5, il résulte que par rapport au polygone de solution, cette droite devient la droite de référence au point C, où la fonction prend sa valeur maximale. Le point C se situe à l'intersection des lignes L 1 et Z 3. Pour déterminer ses coordonnées, on résout le système d'équations :

Plan de tâche optimal = 2,4 ; =1,4. En substituant les valeurs et dans la fonction linéaire, on obtient :

3 2,4 + 4 1,4 = 12,8.

La solution résultante signifie que le volume de production du produit P doit être égal à 2,4 unités et celui du produit P à 1,4 unités. Le revenu perçu dans ce cas sera : Z = 12,8 cu.

Figure 4.5 - Résolution d'un problème de programmation linéaire à l'aide d'une méthode géométrique

5. DOUBLE PROBLÈMES

Composition d'un double problème. Considérons deux problèmes de programmation linéaire :

Maximiser la fonction

sous restrictions

Fonction Réduire

sous restrictions

Ces tâches ont les propriétés suivantes :

1. Dans un problème, on recherche le maximum d'une forme linéaire, et dans l'autre, le minimum.

2°. Les coefficients de variables sous forme linéaire d'un problème sont des membres libres du système de contraintes d'un autre problème ; au contraire, les membres libres du système de contraintes d'un problème sont des coefficients de variables sous forme linéaire d'un autre problème.

3°. Dans chaque problème, un système de contraintes est spécifié sous forme d'inégalités, et elles ont toutes la même signification, à savoir : lorsqu'on trouve le maximum d'une forme linéaire, ces inégalités ont la forme, et lorsqu'on trouve le minimum, elles ont la formulaire

4°. Les coefficients des variables dans les systèmes de contraintes sont décrits par des matrices

qui sont transposés les uns par rapport aux autres.

5°. Le nombre d'inégalités dans le système de contraintes d'un problème coïncide avec le nombre de variables d'un autre problème.

6 f) Les conditions de non-négativité des variables sont préservées dans les deux problèmes.

Deux problèmes de programmation linéaire qui satisfont aux conditions ci-dessus sont appelés problèmes duaux symétriques. Nous n'étudierons que les problèmes duaux symétriques et nous les appellerons donc en abrégé - problèmes duaux.

Ainsi, chaque problème de programmation linéaire peut être associé à son problème dual. Nous appellerons le problème initial le problème initial (ou direct). Le problème direct et son problème double, pris ensemble, forment une paire de problèmes mutuellement duels, et chacun d'entre eux peut être considéré comme le problème initial, alors l'autre lui sera duel.

De ce qui précède, les règles suivantes pour composer un problème double de celui d'origine découlent :

1. Toutes les inégalités du système de contraintes du problème originel se réduisent à des inégalités de même sens : si dans le problème originel on cherche le maximum d'une forme linéaire, à la forme ≤, si le minimum, à la forme ≥. Pour cela, les inégalités pour lesquelles cette condition n’est pas remplie sont multipliées par - 1.

2. Écrivez la matrice A des coefficients des variables du problème d'origine, obtenue après la transformation de l'étape 1, et composez la matrice A" transposée par rapport à la matrice A.

3. Composez un système de restrictions pour le problème dual, en prenant les éléments de la matrice A comme coefficients pour les variables, et les coefficients des variables sous la forme linéaire du problème d'origine comme termes libres, et notez les inégalités du contraire sens par rapport aux inégalités obtenues à l’étape 1.

4. Composez une forme linéaire du problème dual, en prenant les termes libres du système de contraintes du problème original obtenu à l'étape 1 comme coefficients pour les variables.

5. Indiquer ce qu'il faut trouver lors de la résolution d'un problème dual, à savoir : un minimum de forme linéaire si un maximum est recherché dans le problème d'origine, et un maximum si un minimum est recherché dans le problème d'origine.

6. Notez la condition de non-négativité des variables du problème dual.

Exemple 5.1. Créer un problème double du suivant : trouver le maximum d'une fonction sous les contraintes

La troisième inégalité du système (*) ne satisfait pas à la clause 1 des règles de composition d'un problème dual. Multiplions-le donc par –1 :

Pour faciliter la préparation d'un problème dual, il est préférable d'utiliser la matrice étendue B, dans laquelle, avec les coefficients des variables du système de contraintes du problème d'origine, on note les termes libres et les coefficients des variables sous forme linéaire, en mettant en évidence une colonne et une ligne supplémentaires à cet effet. On transpose la matrice B et, à l'aide de la matrice transposée B / , on compose un problème dual à celui-ci.

Le problème dual se réduit à trouver le minimum d'une fonction sous les contraintes

Théorèmes de base de la dualité

La théorie de la dualité en programmation linéaire repose sur les théorèmes de base suivants.

Théorème 1. Si l'un des problèmes de programmation linéaire a un optimal fini, alors son dual a également un optimal fini, et les valeurs optimales des formes linéaires des deux problèmes coïncident, c'est-à-dire F max = Zmin ou F min = Z max . Si la forme linéaire de l’un des problèmes duaux n’est pas limitée, alors les conditions de l’autre problème sont contradictoires.

Avant de formuler le théorème suivant, établissons des correspondances entre les variables du problème original et du problème dual.

Lors de la résolution du problème initial par la méthode du simplexe, pour réduire le système d'inégalités à son système d'équations équivalent, il est nécessaire d'introduire m variables non négatives supplémentaires (en fonction du nombre d'inégalités dans le système de contraintes) où je = 1, 2,…,t désigne le numéro de l'inégalité dans laquelle la variable supplémentaire a été introduite.

Le système de contraintes du problème dual est constitué de n inégalités contenant m variables. Si vous résolvez ce problème en utilisant la méthode du simplexe, vous devez alors introduire n variables non négatives supplémentaires où j = 1, 2,...,m désigne le numéro du système d'inégalité de contraintes du problème dual dans lequel la variable supplémentaire a été présenté.

Établissons la correspondance suivante entre les variables du problème original et du problème dual :

Autrement dit, chaque variable initiale
le problème x j (j = 1,2,…, n) est associé à la variable supplémentaire introduite dans l'inégalité j - e du problème dual, et à chaque variable supplémentaire du problème d'origine (i = 1,2,…, t), introduit dans je- L'inégalité du problème originel, est la variable originelle du problème dual.

Théorème 2 . Les composantes de la solution optimale à l'un des problèmes (direct ou double) sont égales aux valeurs absolues des coefficients des variables correspondantes dans l'expression de la forme linéaire de l'autre problème (dual ou direct) lorsqu'il atteint son optimal et à condition que la solution optimale résultante ne soit pas dégénérée.

Des théorèmes 1 et 2, il s'ensuit que si vous résolvez l'un des problèmes mutuellement duaux, c'est-à-dire trouvez sa solution optimale et l'optimum de la forme linéaire, alors vous pouvez écrire la solution optimale et l'optimum de la forme linéaire du autre problème.

Exemple 5.2. Utilisez la méthode du simplexe pour résoudre les problèmes directs et doubles donnés dans l’exemple précédent.

Solution d'un problème direct. Réduisons le système de contraintes d'inégalité (voir p. 268) à un système d'équations en introduisant des variables supplémentaires non négatives :

Nous prendrons les variables supplémentaires x 3, x 4, x 5, x 6 comme variables principales à la première étape de la solution.

1 étape. Variables principales : x 3, x 4, x 5, x 6 ; variables non principales : x 1, x 2. Exprimons les principales variables en termes de variables non fondamentales (nous ne considérons pas la forme linéaire à cette étape de solution, car la solution de base correspondante n'est pas admissible) :

Pour obtenir une solution de base admissible, nous transformons la variable en solutions de base. On trouve = min (2/1 ; ∞ ; 1/1 ; 5/1) = 1. Dans ce cas, la variable x5 va dans le non-essentiel.

Étape 2. Variables principales : x 1, x 3, x 4, x 6 variables non principales ; x2, x5. Exprimons les principales variables et la forme linéaire en termes de variables non fondamentales :

Convertissons-le en variable principale x5. Croire x5=min (∞ ; 1/1 ; ∞ ; 4/1) = 1, nous concluons que la variable x 3 doit être convertie en non primaire.

Étape 3. Variables principales : x 1, X 4, x 5, x 6, variables mineures x 3, x 2. Nous avons

La variable x 2 est convertie en base. Trouvez x 2 = min (∞; ∞;∞; 1/1)=1. Alors la variable x 6 devient non primaire.

Étape 4. Variables principales : x 1, x 2, X 4,x5, ; variables non principales : x 2, x 6. Nous avons

Le critère d’optimalité est rempli. La solution optimale a la forme (4 ; 1 ; 0 ; 5 ; 4 ; 0) ; avec cette solution F max = 13.

Suite de l'exemple 5.1. On réduit le système de contraintes du problème dual au système d'équations :

Nous prendrons les variables supplémentaires y 5 y 6 comme principales à la 1ère étape de la solution.

1 étape. Principales variables : oui 5, oui 6 ; variables mineures : y 1, y 2, y 3, y 4. Exprimons les principales variables en termes de variables non fondamentales :

Convertissons y en la variable principale 4. On trouve y 4 = mm (3/1 : 1/1 = 1. La variable y 6 entre dans les mineures.

Étape 2. Variables principales : y 4, y 5 variables mineures : y 1, y 2, y 3, y 6. Nous avons

Convertissons la variable y 1 en variables principales. Puisque y 1 = min (∞ ; 2/3) = 2/3, alors la variable y 5 devient non primaire.

Étape 3. Variables principales y 1, y 4, variables mineures : y 2, y 3, y 5, y 6. Puisque la solution de base correspondante au problème est admissible, nous exprimons non seulement les principales en termes de variables non fondamentales, mais aussi sous une forme linéaire :

Le critère d'optimalité (dans le cas de la minimisation d'une forme linéaire) est satisfait. La solution optimale a la forme (2/3 ; 0 ; 0 ; 7/3 ; 0 ; 0), avec Z min = 13.

Après avoir résolu le problème dual, nous sommes convaincus de la validité de la première partie du théorème 1 : le problème dual a aussi un optimum final, et Z min = =Fmax = 13.

Assurons-nous que l'énoncé du Théorème 2 est également vrai. Pour ce faire, nous écrivons les variables des problèmes directs et duaux, en maintenant leur correspondance ;

Exprimons la forme linéaire obtenue à la dernière étape de résolution du problème dual en fonction de toutes les variables de ce problème :

Considérant les coefficients des variables y j sous cette forme linéaire et tenant compte de leur correspondance avec les coefficients des variables XI, on obtient une solution (4 ; 1 ; 0 ; 5 ; 4 ; 0), coïncidant avec la solution optimale du problème direct.

Commentaire. Après avoir résolu le problème direct, vous pouvez immédiatement obtenir une solution au double problème. Si l'on exprime la forme linéaire F obtenue à la 4ème étape de résolution du problème direct en fonction de toutes les variables de ce problème, on obtient

Sur la base du théorème 2, en tenant compte de la correspondance entre les variables dans les problèmes directs et duaux et en prenant la valeur absolue des coefficients des variables, on trouve la solution optimale au problème dual (2/3 ; 0 ; 0 ; 7 /3 ; 0 ; 0). Dans ce cas, Z min = F max = 13.

6 PROBLEME DE TRANSPORT

Ce cas correspond à la contradiction mutuelle des contraintes incluses dans le problème.

2) L'ensemble admissible est un polyèdre borné convexe.

Un ensemble admissible est un ensemble polyédrique convexe non borné.

Les deux derniers cas sont assez faciles à imaginer en deux ou trois dimensions. Dans un espace de dimension supérieure, le concept de polyèdre (ensemble polyédrique) est introduit de manière abstraite comme l'intersection d'hyperplans et d'hyperdemi-plans définis par les équations linéaires correspondantes et les inégalités incluses dans les contraintes du problème. Une propriété caractéristique d'un polyèdre est la présence de points singuliers - pics.

Cas possibles de solutions optimales (plans) pour un problème de programmation linéaire.

1) Problème n'a pas de solutions optimales.

Ce cas peut se présenter : soit lorsque l'ensemble des solutions admissibles est vide (« il n'y a rien à choisir » le plan optimal),

ou lorsque l'ensemble admissible est un ensemble polyédrique illimité et que la fonction objectif sur celui-ci augmente indéfiniment (si L max) ou diminue sans limite (avec Lmin).

2) La tâche a la seule chose solution(le seul plan optimal).

Cette solution coïncide nécessairement avec l'un des sommets de l'ensemble admissible.

3) La tâche a ensemble infini solutions optimales, données par une formation linéaire - une arête, une face, une hyperface, etc. Parmi les points de cette formation linéaire se trouvent également les sommets de l'ensemble admissible.

Ainsi, l'énoncé principal de la théorie de la programmation linéaire, qui détermine en fin de compte les moyens spécifiques de la résoudre, peut être formulé comme suit :

Si un problème de programmation linéaire a au moins un plan optimal, alors il doit être recherché parmi les sommets de l’ensemble admissible de solutions.

Dans la section suivante, les principes généraux abordés seront illustrés à l’aide de l’exemple d’un problème de programmation linéaire à deux variables.

1. Méthode graphique-analytique pour résoudre des problèmes de programmation linéaire

La méthode grapho-analytique (graphique) de résolution de problèmes de programmation linéaire est généralement utilisée pour résoudre des problèmes à deux variables, lorsque les contraintes sont exprimées par des inégalités, ainsi que des problèmes pouvant être réduits à de tels problèmes.

Soit le problème de programmation linéaire de la forme :

(1.7)

Où Avec 1 , Avec 2 , UN je 1, UN je 2, b je - étant donné des nombres réels ; les signes des inégalités sont arbitraires ; la fonction objectif est soit maximisée, soit minimisée.

Chacune des inégalités (1.7) du système de contraintes du problème définit respectivement géométriquement le demi-plan avec les droites limites
;je=1,…,m. Si le système d'inégalités (1.7) est cohérent, le domaine réalisable de solutions au problème est l'ensemble des points appartenant à tous les demi-plans indiqués. L'ensemble des points d'intersection de ces demi-plans étant convexe, la plage de valeurs admissibles est un ensemble convexe, que l'on appelle polygone les décisions. Les côtés de ce polygone reposent sur des droites dont les équations sont obtenues à partir du système de contraintes original en remplaçant les signes d'inégalité par des signes d'égalité.

L’ensemble des solutions réalisables pour ce problème particulier peut être :

zone vide;

polygone convexe, y compris les cas dégénérés - segment de ligne et point unique ;

région polygonale convexe illimitée, y compris les cas dégénérés - rayon et ligne.

La mise en œuvre pratique de la résolution du problème de programmation linéaire (1.6) – (1.7) basée sur son interprétation géométrique comprend les étapes suivantes :

1. Construire des droites dont les équations sont obtenues en remplaçant les signes d'inégalité dans les restrictions (1.7) par des signes égaux.

2. Trouver les demi-plans définis par chacune des contraintes.

Le demi-plan correspondant peut être trouvé en remplaçant un point « simple » dans l'inégalité de coordonnées - (0,0), (0,1) ou (1,0). L'essentiel est que ce point n'appartient pas à la limite du demi-plan. Si après substitution l'inégalité s'avère vraie, alors le demi-plan contenant ce point est sélectionné. Si l’inégalité n’est pas vraie, alors un demi-plan alternatif est sélectionné.

3. Définissez le polygone de solution comme l'intersection des demi-plans trouvés.

4. Construire le gradient de la fonction objectif, c'est-à-dire vecteur
, dont les coordonnées sont les coefficients de la fonction objectif L.

Ce vecteur détermine la direction de l'augmentation la plus rapide de la fonction objectif.

5. Construire une série de lignes de niveau de fonction objectif L, c'est à dire. lignes droites perpendiculaires au dégradé L. Dans ce cas, la construction des lignes de niveau doit être réalisée dans le sens de la pente si l'on résout le problème maximum, et dans le sens opposé (dans le sens de « l'anti-dégradé ») si l'on résout le problème minimum. résolu. En conséquence, le(s) point(s) sont marqués auxquels les lignes de niveau touchent en dernier lieu l'ensemble admissible.

Si l'ensemble admissible est illimité, il se peut qu'il n'y ait pas de point de contact final. Les lignes de niveau vont à l'infini, donc la valeur
ou
, et le problème n'a pas de plans optimaux.

Déterminez analytiquement les coordonnées du point marqué en résolvant le système d’équations linéaires correspondant. Calculez ensuite la valeur de la fonction objectif à ce stade. Ainsi, le plan optimal et la valeur optimale de la fonction objectif du problème sont déterminés.

En conclusion de notre examen de l'interprétation géométrique du problème (1.6) – (1.7), nous notons que lors de la recherche de sa solution, les cas présentés sur la Fig. 1.1 – 1.3. Riz. 1.1 caractérise le cas où la fonction objectif prend une valeur optimale en un seul point A, l'un des sommets de l'ensemble admissible. En figue. 1.2, la fonction objectif prend sa valeur optimale en tout point du segment AB. En figue. La figure 1.3 montre le cas où la valeur optimale de la fonction objectif est inaccessible.

Riz. 1.1. Fonctionnement optimal L accessible au point A

Riz. 1.2. Fonctionnement optimal L est atteint en tout point du segment UN B

Riz. 1.3. Fonctionnement optimal L inaccessible