So finden Sie die optimale Lösung für den Produktionsprozess. Welche Lösung kann als optimal angesehen werden? Grafisch-analytische Methode zur Lösung linearer Programmierprobleme

Es ist zu beachten, dass Methoden zur Lösung linearer Programmierprobleme Folgendes umfassen: nicht für die Wirtschaftswissenschaften, sondern für Mathematik und Computertechnologie. Gleichzeitig muss der Wirtschaftswissenschaftler mit der entsprechenden Software möglichst komfortable Dialogbedingungen schaffen. Solche Bedingungen können wiederum nur durch sich dynamisch entwickelnde und interaktive Entwicklungsumgebungen geschaffen werden, die über eine Reihe von Bibliotheken verfügen, die zur Lösung solcher Probleme erforderlich sind. Eine dieser Softwareentwicklungsumgebungen ist definitiv Python.

Formulierung des Problems

In den Veröffentlichungen wurden Lösungen für direkte Optimierungsprobleme mithilfe der linearen Programmiermethode untersucht und eine sinnvolle Wahl des Scipy-Lösers vorgeschlagen. optimieren.

Es ist jedoch bekannt, dass jedes lineare Programmierproblem einem sogenannten distinguierten (dualen) Problem entspricht. Darin werden im Vergleich zum direkten Problem Zeilen zu Spalten, Ungleichungen ändern das Vorzeichen, statt eines Maximums wird ein Minimum gesucht (oder umgekehrt, statt eines Minimums wird ein Maximum gesucht). Die zum Dualen duale Aufgabe ist die ursprüngliche Aufgabe selbst.

Die Lösung des dualen Problems ist für die Analyse der Ressourcennutzung sehr wichtig. In dieser Veröffentlichung wird bewiesen, dass die optimalen Werte der Zielfunktionen im Original- und Dualproblem übereinstimmen (d. h. das Maximum im Originalproblem fällt mit dem Minimum im Dualproblem zusammen).

Die optimalen Werte der Material- und Arbeitskosten werden anhand ihres Beitrags zur Zielfunktion bewertet. Das Ergebnis werden „objektiv ermittelte Schätzungen“ von Rohstoffen und Arbeitskräften sein, die nicht mit den Marktpreisen übereinstimmen.

Lösung des direkten Problems des optimalen Produktionsprogramms

Angesichts der hohen mathematischen Ausbildung der überwiegenden Mehrheit der Benutzer dieser Ressource werde ich keine Bilanzgleichungen mit oberen und unteren Einschränkungen und der Einführung zusätzlicher Variablen zum Übergang zu Gleichheiten vorstellen. Daher gebe ich gleich die Bezeichnungen der in der Lösung verwendeten Variablen an:
N – Anzahl der hergestellten Produkttypen;
m – Anzahl der verwendeten Rohstoffarten;
b_ub – Vektor der verfügbaren Ressourcen der Dimension m;
A_ub ist eine Matrix der Dimension m×N, deren jedes Element den Verbrauch einer Ressource vom Typ i für die Produktion einer Produkteinheit vom Typ j darstellt;
c ist der Gewinnvektor aus der Produktion einer Einheit jedes Produkttyps;
x – die erforderlichen Mengen an produzierten Produkten jeder Art (optimaler Produktionsplan), um maximalen Gewinn zu gewährleisten.

Zielfunktion
maxF(x)=c×x

Einschränkungen
A×x≤b

Numerische Werte von Variablen:
N=5; m=4; b_ub = ; A_ub = [, , ,]; c = .

Aufgaben
1. Finden Sie x, um den maximalen Gewinn sicherzustellen
2. Finden Sie die Ressourcen, die bei der Durchführung von Schritt 1 verwendet wurden
3. Suchen Sie die verbleibenden Ressourcen (falls vorhanden), wenn Sie Schritt 1 ausführen

Um das Maximum zu bestimmen (standardmäßig wird das Minimum bestimmt), müssen die Koeffizienten der Zielfunktion mit einem negativen Vorzeichen c = [-25, -35,-25,-40,-30] geschrieben werden und das Minuszeichen ignorieren vor dem Gewinn.

Zur Anzeige der Ergebnisse verwendete Notationen:
X– ein Array variabler Werte, die das Minimum (Maximum) der Zielfunktion liefern;
locker– Werte zusätzlicher Variablen. Jede Variable entspricht einer Ungleichheitsbeschränkung. Ein Variablenwert von Null bedeutet, dass die entsprechende Einschränkung aktiv ist;
Erfolg– True, wenn es der Funktion gelungen ist, die optimale Lösung zu finden;
Status– Entscheidungsstatus:
0 – die Suche nach der optimalen Lösung wurde erfolgreich abgeschlossen;
1 – die Grenze der Anzahl der Iterationen wurde erreicht;
2 – das Problem hat keine Lösungen;
3 – Die Zielfunktion ist nicht eingeschränkt.
nit– Anzahl der durchgeführten Iterationen.

Auflistung der Lösung des direkten Optimierungsproblems

#!/usr/bin/python # -*- Codierung: utf-8 -*- Import scipy from scipy.optimize import linprog # Laden der LP-Bibliothek c = [-25, -35,-25,-40,-30] # Liste der Koeffizienten der Zielfunktion b_ub = # Liste der Ressourcenvolumina A_ub = [, # Matrix spezifischer Ressourcenwerte , , ] d=linprog(c, A_ub, b_ub) # Suche nach einer Lösung für key,val in d.items(): print(key ,val) # Lösungsausgabe if key=="x": q=#used resources print("A_ub*x",q) q1= scipy.array(b_ub)-scipy.array (q) #verbleibende Ressourcen print(" b_ub-A_ub*x", q1)

Ergebnisse der Lösung des Problems
nit 3
Status 0

Erfolg Stimmt
x [ 0. 0. 18.18181818 22.72727273 150. ]
A_ub*x
b_ub-A_ub*x [0. 0. 0. 90.90909091]
Spaß -5863.63636364
locker [0. 0. 0. 90.90909091]

Schlussfolgerungen

Der optimale Plan für die Produkttypen wurde gefunden
Tatsächliche Ressourcennutzung gefunden
Der Rest des ungenutzten vierten Ressourcentyps wurde gefunden [ 0, 0 0,0 0,0 90,909]
Berechnungen gemäß Schritt 3 sind nicht erforderlich, da das gleiche Ergebnis in der Slack-Variable angezeigt wird

Lösung des dualen Problems zum optimalen Produktionsprogramm

Der vierte Ressourcentyp in der direkten Aufgabe wird nicht vollständig genutzt. Dann stellt sich heraus, dass der Wert dieser Ressource für das Unternehmen im Vergleich zu Ressourcen, die die Produktion begrenzen, geringer ist und das Unternehmen bereit ist, einen höheren Preis für den Erwerb von Ressourcen zu zahlen, die den Gewinn steigern.

Lassen Sie uns einen neuen Zweck für die gewünschte Variable x als einen „Schattenpreis“ einführen, der den Wert einer bestimmten Ressource im Verhältnis zum Gewinn aus dem Verkauf hergestellter Produkte bestimmt.

C – Vektor der verfügbaren Ressourcen;
b_ub ist der Gewinnvektor aus der Produktion einer Einheit jedes Produkttyps;
A_ub_T – transponierte Matrix A_ub.

Zielfunktion
minF(x)=c×x

Einschränkungen
A_ub_T ×x≥ b_ub

Numerische Werte und Beziehungen für Variablen:
c = ; A_ub_T transpose(A_ub); b_ub = .

Aufgabe:
Finden Sie x, das den Wert für den Produzenten jedes Ressourcentyps angibt.

Merkmale der Lösung mit der Scipy-Bibliothek. optimieren
Um Einschränkungen von oben durch Einschränkungen von unten zu ersetzen, müssen beide Teile der Einschränkung mit minus eins multipliziert werden – A_ub_T ×x≥ b_ub... Schreiben Sie dazu die Anfangsdaten in der Form: b_ub = [-25, -35,-25,-40,-30]; A_ub_T =- scipy.transpose(A_ub).

Auflistung der Lösung des dualen Optimierungsproblems

#!/usr/bin/python # -*- Codierung: utf-8 -*- scipy aus scipy.optimize importieren linprog importieren A_ub = [, , , ] c= b_ub = [-25, -35,-25,- 40,-30] A_ub_T =-scipy.transpose(A_ub) d=linprog(c, A_ub_T, b_ub) für key,val in d.items(): print(key,val)

Ergebnisse der Lösung des Problems
nit 7
Meldung Optimierung erfolgreich beendet.
Spaß 5863.63636364
x [ 2,27272727 1,81818182 6,36363636 0. ]
locker [5.45454545 2.27272727 0. 0. 0. ]
Status 0
Erfolg Stimmt

Schlussfolgerungen

Der dritte Ressourcentyp hat für den Hersteller den größten Wert, daher sollte dieser Ressourcentyp zuerst gekauft werden, dann der erste und der zweite Ressourcentyp. Der vierte Ressourcentyp hat für den Hersteller keinen Wert und wird zuletzt gekauft.

Ergebnisse des Vergleichs direkter und dualer Probleme

Das duale Problem erweitert die Möglichkeiten der Produktplanung, jedoch mit Scipy. Optimize wird in der doppelten Anzahl direkter Iterationen gelöst.
Die Slack-Variable stellt Informationen über die Aktivität von Einschränkungen in Form von Ungleichungen dar, die beispielsweise zur Analyse von Rohstoffbilanzen verwendet werden können.
Das direkte Problem ist ein Maximierungsproblem und das duale Problem ist ein Minimierungsproblem und umgekehrt.
Die Koeffizienten der Zielfunktion im direkten Problem sind Einschränkungen im dualen Problem.
Einschränkungen im direkten Problem werden zu Koeffizienten der Zielfunktion im dualen Problem.
Die Vorzeichen der Ungleichheiten bei den Beschränkungen kehren sich um.
Die Matrix des Gleichheitssystems wird transponiert.

Links Es wird eine Optimierung linearer Modelle in MS Excel durchgeführt Simplex-Methode- gezielte Suche nach Referenzlösungen für ein lineares Programmierproblem. Der Algorithmus der Simplex-Methode besteht darin, ein konvexes Polyeder in einem mehrdimensionalen Raum zu konstruieren und dann seine Eckpunkte aufzuzählen, um einen Extremwert zu finden Zielfunktion.

Wirksame Mittel Lineares Programmieren bilden die Grundlage sowohl der ganzzahligen als auch der nichtlinearen Programmierung zur Lösung komplexerer Optimierungsprobleme. Diese Methoden erfordern jedoch längere Rechenzeiten.

In den weiteren Vorträgen werden Beispiele zur Lösung typischer Optimierungsprobleme und zur Entscheidungsfindung mit dem MS Excel-Add-in „Lösung suchen“ ausführlich besprochen. Die Aufgaben, die dieses Tool am besten löst, haben drei Haupteigenschaften:

es gibt ein einzelnes Ziel, das funktional mit anderen Parametern des Systems zusammenhängt und optimiert werden muss (um sein Maximum, Minimum oder einen bestimmten numerischen Wert zu finden);
Es gibt Einschränkungen, die sich meist in Form von Ungleichheiten äußern (z. B. darf die Menge der eingesetzten Rohstoffe den Bestand an Rohstoffen im Lager nicht überschreiten, oder die Betriebszeit einer Maschine pro Tag darf nicht mehr als 24 Stunden abzüglich Wartung betragen Zeit);
Es gibt eine Reihe von Eingabevariablenwerten, die die optimierten Werte und Einschränkungen beeinflussen.

Die Parameter der Aufgaben sind auf folgende Grenzindikatoren beschränkt:

Anzahl der Unbekannten – 200;
Anzahl formelhafter Einschränkungen für Unbekannte – 100;
die Anzahl der Randbedingungen für Unbekannte beträgt 400.

Der Algorithmus zum Finden optimaler Lösungen umfasst mehrere Phasen:

Vorarbeit;
Debuggen der Lösung;
Lösungsanalyse.

Der Ablauf der notwendigen Vorarbeiten zur Lösung wirtschaftlicher und mathematischer Modellierungsprobleme mit MS Excel ist im Blockdiagramm in Abbildung 1.6 dargestellt.

Reis. 1.6.

Von den fünf Punkten des vorbereitenden Arbeitsplans ist nur der fünfte Punkt formalisierbar. Der Rest der Arbeit erfordert Kreativität – und verschiedene Menschen können sie auf unterschiedliche Weise erledigen. Lassen Sie uns kurz den Kern des Wortlauts der Planpunkte erläutern.

Bei der Problemstellung sind die Zielkoeffizienten und die normalisierten Koeffizienten bekannt. Im vorherigen Beispiel waren die Koeffizienten, die die Zielfunktion bilden, die Werte des normalisierten Gewinns pro Regal vom Typ ( ) und ein Regaltyp ( ). Die normalisierten Koeffizienten waren die Normen des Materialverbrauchs und der Maschinenzeit pro Regal jedes Typs. Die Matrix sah so aus:

Darüber hinaus sind die Ressourcenwerte stets bekannt. Im vorherigen Beispiel handelte es sich um einen Wochenvorrat an Platinen und die Möglichkeit, Maschinenzeit zu nutzen: , . Bei Problemen müssen häufig die Werte von Variablen begrenzt werden. Daher ist es notwendig, die Unter- und Obergrenzen des Bereichs ihrer Änderungen zu bestimmen.

Daher müssen wir im Dialogfenster des Optimierungsprogramms „Lösung suchen“ folgenden Zielalgorithmus einstellen:

Die Zielfunktion ist gleich dem Produkt des Vektors der gewünschten Variablenwerte mit dem Vektor der Zielkoeffizienten

Die normalisierten Koeffizienten für den Vektor der erforderlichen Variablenwerte sollten den Wert des angegebenen Ressourcenvektors nicht überschreiten

Die Variablenwerte müssen innerhalb der angegebenen Grenzen der Anzahl der Anfangselemente des Systems liegen

Anzahl der Anfangselemente des Systems

Anzahl der angegebenen Ressourcentypen

Das Debuggen der Lösung ist erforderlich, wenn das Programm eine Meldung über negative Ergebnisse anzeigt (Abbildung 1.7):

Reis. 1.7.

Wenn keine akzeptable Lösung erzielt wird, passen Sie das Quelldatenmodell an.
wenn nicht erhalten optimale Lösung, und führen Sie dann zusätzliche Einschränkungen ein.

Die Programmprobleme optimale Lösung nur für ein Modell des realen Problems und nicht für eine Lösung des Problems selbst. Bei der Erstellung des Modells wurden verschiedene vereinfachende Annahmen über die reale Situation getroffen. Dadurch war es möglich, den Prozess zu formalisieren und reale quantitative Beziehungen zwischen den Systemparametern und dem Ziel näherungsweise abzubilden. Und wenn die realen Parameter von denen im Modell abweichen, wie wird sich dann die Lösung ändern? Um dies herauszufinden, wird vor einer Managemententscheidung eine Analyse der Modelllösung durchgeführt.

Analyse optimale Lösung, in das Programm integriert, stellt die letzte Stufe der mathematischen Modellierung wirtschaftlicher Prozesse dar. Es ermöglicht eine tiefergehende Überprüfung der Prozesskonformität des Modells sowie der Zuverlässigkeit der optimalen Lösung. Es basiert auf Daten optimale Lösung und Berichte, die im Rahmen der „Lösungssuche“ ausgegeben werden. Es schließt jedoch die traditionelle Analyse des Plans aus wirtschaftlicher Sicht vor einer Managemententscheidung nicht aus und ersetzt sie auch nicht.

Die Wirtschaftsanalyse hat folgende Ziele:

Ermittlung möglicher Konsequenzen im Gesamtsystem und seinen Elementen bei Änderung eines Modellparameters;
Einschätzung der Stabilität des optimalen Plans gegenüber Änderungen einzelner Parameter des Problems: Wenn er gegenüber Änderungen der meisten Parameter nicht stabil ist, wird die Garantie für seine Umsetzung und das Erreichen des berechneten Optimums verringert;
Variantenrechnungen durchzuführen und neue Planoptionen zu gewinnen, ohne das Problem von der ursprünglichen Basis durch Anpassungen neu zu lösen.

Mögliche Analysemethoden sind im Diagramm in Abbildung 1.8 dargestellt.

Nachdem die optimale Lösung gefunden wurde, wird diese anhand der erhaltenen Berichte analysiert. Stabilitätsanalyse- Untersuchung des Einflusses von Änderungen einzelner Modellparameter auf die Indikatoren der optimalen Lösung. Grenzwertanalyse- Analyse zulässiger Änderungen im optimalen Plan, bei denen der Plan optimal bleibt.

Angesichts der Verantwortung, wirtschaftliche zu akzeptieren Managemententscheidung, muss der Manager sicherstellen, dass der resultierende optimale Plan der einzig richtige ist. Dazu ist es notwendig, auf Basis des Modells Antworten auf folgende Fragen zu erhalten:

"was passiert wenn…"
„Was braucht es, um…“

Die Analyse zur Beantwortung der ersten Frage wird aufgerufen Variantenanalyse; Die Analyse zur Beantwortung der zweiten Frage wird aufgerufen individuelle Lösungen.

Die Variantenanalyse kann folgender Art sein:

Parametrisch- Analyse, die darin besteht, ein Problem für verschiedene Werte eines bestimmten Parameters zu lösen.
Strukturanalyse- wenn eine Lösung für ein Optimierungsproblem unter einer anderen Struktur von Randbedingungen gesucht wird.
Multikriterielle Analyse ist eine Lösung eines Problems unter Verwendung verschiedener Zielfunktionen.
Analyse mit bedingten Ausgangsdaten- wenn die zur Lösung eines Problems verwendeten Ausgangsdaten von der Einhaltung zusätzlicher Bedingungen abhängig sind.

Nach der Analyse sollen die Ergebnisse grafisch dargestellt und ein Bericht mit Empfehlungen für Entscheidungen unter Berücksichtigung der konkreten Wirtschaftslage erstellt werden.

Eine universelle Methode zur Lösung von LP-Problemen heißt Simplex-Methode. Anwendung dieser Methode und ihrer häufigsten Modifikation – der Zweiphasen-Simplex-Methode.

Bei der grafischen Methode zur Lösung von LP-Problemen haben wir tatsächlich aus der Menge der Scheitelpunkte, die zur Grenze der Lösungsmenge des Ungleichungssystems gehören, den Scheitelpunkt ausgewählt, an dem der Wert der Zielfunktion ein Maximum (Minimum) erreicht. Bei zwei Variablen ist diese Methode völlig intuitiv und ermöglicht eine schnelle Lösung des Problems.

Wenn ein Problem drei oder mehr Variablen hat und dies bei realen Wirtschaftsproblemen genau der Fall ist, ist es schwierig, den Lösungsbereich des Zwangssystems zu visualisieren. Solche Probleme werden mit gelöst Simplex-Methode oder durch die Methode der sukzessiven Verbesserungen. Die Idee der Methode ist einfach und lautet wie folgt.

Gemäß einer bestimmten Regel wird der anfängliche Referenzplan (ein gewisser Scheitelpunkt des Einschränkungsbereichs) gefunden. Es prüft, ob der Plan optimal ist. Wenn ja, dann ist das Problem gelöst. Wenn nicht, gehen wir zu einem anderen verbesserten Plan über – zu einem anderen Höhepunkt. Der Wert der Zielfunktion auf dieser Ebene (an diesem Scheitelpunkt) ist offensichtlich besser als in der vorherigen. Der Übergangsalgorithmus wird mithilfe eines bestimmten Rechenschritts ausgeführt, der zweckmäßigerweise in Form von sogenannten Tabellen geschrieben wird Simplex-Tabellen . Da es eine endliche Anzahl von Knoten gibt, gelangen wir in einer endlichen Anzahl von Schritten zur optimalen Lösung.

Betrachten wir die Simplex-Methode anhand eines konkreten Beispiels für das Problem der Planerstellung.

Beachten wir noch einmal, dass die Simplex-Methode auf die Lösung kanonischer LP-Probleme anwendbar ist, die auf eine spezielle Form reduziert sind, d. h. mit einer Basis, positiven rechten Seiten und einer Zielfunktion, ausgedrückt durch nicht-Basisvariablen. Wenn die Aufgabe nicht auf eine spezielle Form reduziert wird, sind zusätzliche Schritte erforderlich, über die wir später sprechen werden.

Betrachten wir das Problem eines Produktionsplans, nachdem wir zuvor ein Modell konstruiert und in eine spezielle Form gebracht haben.

Aufgabe.

Zur Herstellung von Produkten A Und IN Das Lager kann nicht mehr als 80 Rohstoffeinheiten freigeben. Darüber hinaus für die Herstellung des Produkts A Es werden zwei Einheiten verbraucht und die Produkte IN- eine Einheit Rohstoffe. Es ist notwendig, die Produktion so zu planen, dass der größtmögliche Gewinn der Produkte gewährleistet ist A Es ist erforderlich, nicht mehr als 50 Stück und Produkte herzustellen IN- nicht mehr als 40 Stück. Darüber hinaus der Gewinn aus dem Verkauf eines Produkts A- 5 Rubel und ab IN- 3 reiben.

Lassen Sie uns ein mathematisches Modell erstellen und bezeichnen X 1 Menge der Produkte A im Plan, z X 2 - Anzahl der Produkte IN. dann sieht das Einschränkungssystem so aus:

x 1 ≤50
x 2 ≤40
2x 1 +x 2 ≤80
x 1 ≥0, x 2 ≥0
5x 1 +3x 2 →max

Bringen wir das Problem in eine kanonische Form, indem wir zusätzliche Variablen einführen:

x 1 +x 3 =50
x 2 +x 4 =40
2x 1 +x 2 +x 5 =80
x 1 ≥0, x 2 ≥0
5x 1 +3x 2 →max
-F = -5x 1 - 3x 2 → min.

Dieses Problem hat eine spezielle Form (mit Basis, die rechten Seiten sind nicht negativ). Es kann mit der Simplex-Methode gelöst werden.

ICHBühne. Aufzeichnen eines Problems in einer Simplex-Tabelle. Es besteht eine Eins-zu-eins-Entsprechung zwischen dem System der Randbedingungen des Problems (3.10) und der Simplex-Tabelle. Es gibt so viele Zeilen in der Tabelle, wie es Gleichheiten im System der Beschränkungen gibt, und es gibt so viele Spalten, wie es freie Variablen gibt. Basisvariablen füllen die erste Spalte, freie Variablen füllen die oberste Zeile der Tabelle. Die unterste Zeile wird Indexzeile genannt; darin werden die Koeffizienten der Variablen der Zielfunktion geschrieben. In der unteren rechten Ecke wird zunächst 0 geschrieben, wenn in der Funktion kein freies Element vorhanden ist; Wenn ja, dann schreiben Sie es mit dem umgekehrten Vorzeichen. An dieser Stelle (in der unteren rechten Ecke) befindet sich ein Wert der Zielfunktion, dessen Absolutwert beim Wechsel von einer Tabelle zur anderen zunehmen sollte. Tabelle 3.4 entspricht also unserem Restriktionssystem und wir können mit Stufe II der Lösung fortfahren.

Tabelle 3.4

Basic			frei

IIBühne. Überprüfung des Referenzplans auf Optimalität.

Diese Tabelle 3.4 entspricht dem folgenden Referenzplan:

(X 1 , X 2 , X 3 , X 4 , X 5) = (0, 0, 50, 40, 80).

Freie Variablen X 1 , X 2 gleich 0; X 1 = 0, X 2 = 0. Und die Grundvariablen X 3 , X 4 , X 5 Werte annehmen X 3 = 50, X 4 = 40, X 5 = 80 – aus der Spalte „Freie Bedingungen“. Zielfunktionswert:

-F = - 5X 1 - 3X 2 = -5 0 - 3 0 = 0.

Unsere Aufgabe ist es zu prüfen, ob ein vorgegebener Referenzplan optimal ist. Dazu müssen Sie sich die Indexzeile ansehen – die Zielfunktionszeile F.

Verschiedene Situationen sind möglich.

1. Im Index F- Die Zeichenfolge enthält keine negativen Elemente. Das bedeutet, dass der Plan optimal ist und eine Lösung des Problems niedergeschrieben werden kann. Die Zielfunktion hat ihren optimalen Wert erreicht, der der Zahl in der unteren rechten Ecke mit umgekehrtem Vorzeichen entspricht. Fahren wir mit Stufe IV fort.

2. Die Indexzeile enthält mindestens ein negatives Element, deren Spalte keine positiven Elemente enthält. Dann kommen wir zu dem Schluss, dass die Zielfunktion F→∞ nimmt unbegrenzt ab.

3. Die Indexzeile enthält ein negatives Element, dessen Spalte mindestens ein positives Element enthält. Dann gehen wir zur nächsten Stufe III über. Wir berechnen die Tabelle neu und verbessern so den Referenzplan.

IIIBühne. Verbesserung des Referenzplans.

Aus den negativen Elementen des Index F-Zeilen, wählen Sie diejenige mit dem größten Modul aus, rufen Sie die entsprechende Spaltenauflösung auf und markieren Sie sie mit „“.

Um eine Auflösungszeile auszuwählen, müssen die Verhältnisse der Elemente der Spalte mit den freien Begriffen berechnet werden nur Zu positiv Elemente der Auflösungsspalte. Wählen Sie aus den erhaltenen Beziehungen die minimale aus. Das entsprechende Element, bei dem das Minimum erreicht wird, wird als Auflösung bezeichnet. Wir werden es mit einem Quadrat hervorheben.

In unserem Beispiel ist Element 2 permissiv. Die diesem Element entsprechende Linie wird auch als Auflösung bezeichnet (Tabelle 3.5).

Tabelle 3.5

Nachdem wir das zulässige Element ausgewählt haben, berechnen wir die Tabelle gemäß den Regeln neu:

1. In einer neuen Tabelle gleicher Größe wie zuvor werden die Variablen der auflösenden Zeile und Spalte vertauscht, was dem Übergang auf eine neue Basis entspricht. In unserem Beispiel: X Stattdessen ist 1 in der Basis enthalten X 5, die die Basis verlässt und nun frei ist (Tabelle 3.6).

Tabelle 3.6

2. Schreiben Sie anstelle des auflösenden Elements 2 seine Umkehrzahl ½.

3. Wir teilen die Elemente der Auflösungslinie durch das Auflösungselement.

4. Wir dividieren die Elemente der Auflösungsspalte durch das Auflösungselement und schreiben sie mit umgekehrtem Vorzeichen.

5. Um die restlichen Elemente der Tabelle 3.6 auszufüllen, führen wir eine Neuberechnung mit der Rechteckregel durch. Nehmen wir an, wir möchten das Element an Position 50 zählen.

Wir verbinden dieses Element gedanklich mit dem auflösenden, finden das Produkt und subtrahieren das Produkt der Elemente, die sich auf der anderen Diagonale des resultierenden Rechtecks befinden. Wir dividieren die Differenz durch das auflösende Element.

Also, . Wir schreiben 10 an die Stelle, an der 50 waren. Ähnlich:
, , , .

Tabelle 3.7

Wir haben eine neue Tabelle 3.7, die Grundvariablen sind jetzt die Variablen (x 3,x 4,x 1). Der Wert der Zielfunktion wurde zu -200, d. h. verringert. Um diese Grundlösung auf Optimalität zu prüfen, müssen wir noch einmal zu Stufe II übergehen. Der Prozess ist offensichtlich endlich; das Abbruchkriterium sind die Punkte 1 und 2 der Stufe II.

Lassen Sie uns die Lösung des Problems abschließen. Dazu überprüfen wir die Indexzeile und rufen, wenn wir darin ein negatives Element -½ sehen, die entsprechende Spaltenauflösung auf und berechnen gemäß Stufe III die Tabelle neu. Nachdem wir die Beziehungen zusammengestellt und das Minimum = 40 ausgewählt haben, haben wir das auflösende Element 1 bestimmt. Jetzt führen wir die Neuberechnung gemäß den Regeln 2-5 durch.

Tabelle 3.8

Nach der Neuberechnung der Tabelle stellen wir sicher, dass sich in der Indexzeile keine negativen Elemente befinden. Damit ist das Problem gelöst und der Grundplan optimal.

IVBühne. Die optimale Lösung aufschreiben.

Wenn das Simplex-Verfahren gemäß Punkt 1 der Stufe II gestoppt wurde, wird die Lösung des Problems wie folgt ausgeschrieben. Die Basisvariablen übernehmen entsprechend die Werte der Dummy-Terms-Spalte. In unserem Beispiel X 3 = 30, X 2 = 40, X 1 = 20. Freie Variablen sind 0, X 5 = 0, X 4 = 0. Die Zielfunktion nimmt den Wert des letzten Elements der Spalte der freien Terme mit dem umgekehrten Vorzeichen an: - F = -220 → F= 220, in unserem Beispiel wurde die Funktion bei min und zunächst untersucht F→ max, also hat sich das Vorzeichen tatsächlich zweimal geändert. Also, X* = (20, 40, 30, 0, 0), F* = 220. Antwort auf die Aufgabe:

Es ist notwendig, 20 Produkte dieses Typs in den Produktionsplan aufzunehmen A, 40 Produkte vom Typ B, wobei der Gewinn maximal ist und 220 Rubel beträgt.

Am Ende dieses Abschnitts präsentieren wir ein Flussdiagramm des Algorithmus der Simplex-Methode, das die Schritte genau wiederholt, für einige Leser jedoch möglicherweise bequemer zu verwenden ist, da die Pfeile eine klare Aktionsrichtung anzeigen.

Die Links über den Kästchen im Flussdiagramm geben an, zu welcher Stufe oder Unterpunkt die entsprechende Gruppe von Transformationen gehört. Die Regel für die Ermittlung des ursprünglichen Referenzplans wird in Abschnitt 3.7 formuliert.

Beispiel. Lösen Sie das folgende LP-Problem in kanonischer Form mit der Simplex-Methode.
f(x)=x 1 +9x 2 +5x 3 +3x 4 +4x 5 +14x 6 → min
x 1 +x 4 =20
x 2 +x 5 =50
x 3 +x 6 =30
x 4 +x 5 +x 6 =60
x i ≥ 0, i = 1,…,6
Ein LP-Problem hat eine kanonische Form, wenn alle Einschränkungen (mit Ausnahme der Bedingungen für die Nichtnegativität von Variablen) die Form von Gleichheiten haben und alle freien Terme nicht negativ sind. Wir haben also das Problem in kanonischer Form.
Die Idee der Simplex-Methode ist wie folgt. Zuerst müssen Sie einen (anfänglichen) Scheitelpunkt des Polyeders zulässiger Lösungen finden (anfängliche zulässige Basislösung). Dann müssen Sie diese Lösung auf Optimalität prüfen. Wenn es optimal ist, wurde eine Lösung gefunden; Wenn nicht, gehen Sie zu einem anderen Scheitelpunkt des Polyeders und prüfen Sie erneut die Optimalität. Aufgrund der Endlichkeit der Eckpunkte des Polyeders (eine Folge der Endlichkeit der Einschränkungen des LP-Problems) werden wir in einer endlichen Anzahl von „Schritten“ den erforderlichen Minimal- oder Maximalpunkt finden. Es ist zu beachten, dass beim Übergang von einem Scheitelpunkt zum anderen der Wert der Zielfunktion abnimmt (beim Minimalproblem) oder zunimmt (beim Maximalproblem).
Somit basiert die Idee der Simplex-Methode auf drei Eigenschaften des LP-Problems.
Lösung. Um die anfängliche zulässige Basislösung zu finden, d. h. Zur Bestimmung der Basisvariablen muss das System (5.6) auf eine „diagonale“ Form reduziert werden. Mit der Gaußschen Methode (Methode der sequentiellen Eliminierung von Unbekannten) erhalten wir aus (5.6):
x 2 +x 1 +x 3 =40
x 4 +x 1 =20
x 5 -x 1 -x 3 =10
x 6 +x 3 =30
Daher sind die Grundvariablen x 2 , x 4 , x 5 , x 6 , Wir geben ihnen Werte, die den freien Mitgliedern der entsprechenden Strings entsprechen: x 2 =40, x 4 =20, x 5 =10, x 6 =30,. Variablen x 1 Und x 3 sind nicht grundlegend: x 1 =0, x 3 =0.
Konstruieren wir die erste realisierbare Grundlösung
x 0 = (0,40,0,20,10,30) (5,9)
Um die Optimalität der gefundenen Lösung zu überprüfen x 0 Es ist notwendig, Basisvariablen von der Zielfunktion auszuschließen (unter Verwendung von System (5.8)) und eine spezielle Simplex-Tabelle zu erstellen.
Nach dem Eliminieren von Variablen ist es praktisch, die Zielfunktion in der Form zu schreiben:
f(x) = -7x 1 – 14x 3 +880 (5.10)
Unter Verwendung von (5.8)–(5.10) erstellen wir nun die anfängliche Simplex-Tabelle:

Die Nulllinie enthält die Koeffizienten mit umgekehrtem Vorzeichen der entsprechenden Variablen für die Zielfunktion. Optimalitätskriterium (für das minimale Suchproblem): zulässige Basislösung( x 0) ist optimal, wenn es keine einzige streng positive Zahl in der Nulllinie gibt (ohne Berücksichtigung des Werts der Zielfunktion (880)). Diese Regel gilt auch für nachfolgende Iterationen (Tabellen). Die Elemente der nullten Zeile werden als Spaltenschätzungen bezeichnet.
Die zunächst zulässige Basislösung (5.9) ist also suboptimal: 7>0, 14>0 .
Die Nullspalte enthält die Werte der Basisvariablen. Sie dürfen nicht negativ sein (siehe Gleichung (5.7)). Die Koeffizienten der Variablen aus System (5.8) werden von der ersten bis vierten Zeile geschrieben.
Als x 0 nicht optimal ist, müssen wir zu einem anderen Scheitelpunkt des Polyeders der zulässigen Lösungen wechseln (einen neuen d.b.r. konstruieren). Dazu müssen Sie das führende Element finden und eine bestimmte Transformation (Simplex-Transformation) durchführen.
Zuerst finden wir das führende Element der Tabelle, das am Schnittpunkt der führenden Spalte (der Spalte mit der höchsten positiven Punktzahl) und der führenden Zeile (der Zeile, die dem Mindestverhältnis der Elemente der Nullspalte entspricht) steht entsprechenden Elemente (streng positiv) der führenden Spalte).
In Tabelle 1 ist die führende Spalte die dritte Spalte und die führende Zeile die vierte Zeile. (min(40/1,30/1)=30/1) sind durch Pfeile und das führende Element durch einen Kreis gekennzeichnet. Das führende Element gibt an, dass es sich um die zugrunde liegende Variable handelt x 6 muss durch ein nicht grundlegendes ersetzt werden x 3. Dann werden die neuen Grundvariablen sein x 2 , x 3 , x 4 , x 5 , und nicht grundlegend - x1, x6,. Dies bedeutet den Übergang zu einem neuen Scheitelpunkt des Polyeders zulässiger Lösungen. Um die Koordinatenwerte einer neuen zulässigen Basislösung zu finden x00 Sie müssen eine neue Simplex-Tabelle erstellen und darin elementare Transformationen durchführen:
A) Teilen Sie alle Elemente der führenden Linie durch das führende Element, wodurch das führende Element in 1 umgewandelt wird (zur Vereinfachung der Berechnung).
B) unter Verwendung des führenden Elements (gleich 1) alle Elemente der führenden Spalte in Nullen umwandeln (ähnlich der Methode zum Eliminieren von Unbekannten);
Dadurch erhält man in der Nullspalte die Werte neuer Basisvariablen x 2 , x 3 , x 4 , x 5 ,(siehe Tabelle 2) - Grundkomponenten des neuen Scheitelpunkts x00(Nicht-Basiskomponenten x 1 =0, x 6 =0,).

Wie Tabelle 2 zeigt, handelt es sich um die neue Basislösung x 00 =(0,10,30,20,40,0) suboptimal (die Nulllinie enthält einen nicht negativen Wert von 7). Daher erstellen wir mit dem führenden Element 1 (siehe Tabelle 2) eine neue Simplex-Tabelle, d.h. Konstruieren Sie eine neue realisierbare Grundlösung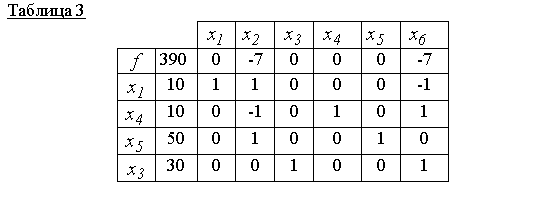

Tabelle 3 entspricht einer akzeptablen Grundlösung x 000 =(10,0,30,10,50,0) und es ist optimal, weil In der Nulllinie gibt es keine positiven Bewertungen. Deshalb f(x 000)=390 ist der Minimalwert der Zielfunktion.
Antwort: x 000 =(10, 0, 30, 10, 50, 0)- Mindestpunktzahl, f(x 000)=390.

Herkömmliches Standardproblem der linearen Programmierung

Sie müssen die folgenden Aufgaben in der angegebenen Reihenfolge ausführen.

Finden Sie den optimalen Plan für das direkte Problem:
a) grafische Methode;
b) Verwendung der Simplex-Methode (zur Erstellung des anfänglichen Referenzplans wird empfohlen, die Methode der künstlichen Basis zu verwenden).
Konstruieren Sie ein duales Problem.
Finden Sie den optimalen Plan für das duale Problem aus der grafischen Lösung der Geraden unter Verwendung der Bedingungen der komplementären Slackness.
Finden Sie den optimalen Plan für das duale Problem unter Verwendung des ersten Dualitätssatzes und unter Verwendung der endgültigen Simplex-Tabelle, die Sie durch Lösen des direkten Problems erhalten (siehe Abschnitt 1b). Überprüfen Sie die Aussage „Die Werte der Zielfunktionen eines Paares dualer Probleme stimmen in ihren optimalen Lösungen überein.“
Lösen Sie das duale Problem mit der Simplex-Methode und finden Sie dann mithilfe der endgültigen Simplex-Tabelle des dualen Problems mithilfe des ersten Dualitätssatzes den optimalen Plan für das direkte Problem. Vergleichen Sie das Ergebnis mit dem grafisch ermittelten Ergebnis (siehe Absatz 1a).
Finden Sie die optimale ganzzahlige Lösung:
a) grafische Methode;
b) Gomori-Methode.
Vergleichen Sie die Werte ganzzahliger und nicht ganzzahliger Lösungsfunktionen

Fragen zur Selbstkontrolle

Wie ist ein Simplex-Tisch aufgebaut?
Wie spiegelt sich eine Änderung der Basis in der Tabelle wider?
Formulieren Sie ein Abbruchkriterium für die Simplex-Methode.
Wie organisiere ich die Neuberechnung einer Tabelle?
Welche Zeile ist geeignet, um mit der Neuberechnung der Tabelle zu beginnen?

Wenn sich bei dem gerade betrachteten Problem die erste gefundene Grundlösung als zulässig herausstellte, kann sie in anderen Fällen nicht sofort, sondern nach einer bestimmten Anzahl von Schritten gefunden werden.

Es muss daran erinnert werden, dass in der ersten Phase der Simplex-Methode, d. h. bei der Suche nach einer möglichen Lösung, die lineare Form nicht berücksichtigt wird und sich alle Transformationen nur auf das System von Einschränkungen beziehen.

Das Problem der linearen Programmierung sei in allgemeiner Form gegeben, d. h. System von m linearen Gleichungen mit n Variablen (m

Folglich entspricht diese Methode der Aufteilung von Variablen in Basis- und Nicht-Basisvariablen der Basislösung...; 0; 0;…;0.

Betrachten wir den allgemeinen Fall, dass diese Lösung nicht akzeptabel ist. Von der erhaltenen Basislösung muss zunächst zu einer zulässigen Basislösung übergegangen werden, und es ist nicht notwendig, dass dieser Übergang sofort, in einem Schritt, durchgeführt wird.

Wenn das System der Randbedingungen nicht inkonsistent ist, erfolgt nach einer endlichen Anzahl von Schritten der Übergang zu einer zulässigen Basislösung.

Aufgrund der Annahme ist die ursprüngliche Grundlösung ungültig. Folglich gibt es unter den freien Gliedern des Zwangssystems mindestens ein negatives (die Zahl der negativen freien Glieder dieses Systems stimmt mit der Zahl der negativen Komponenten der ursprünglichen Grundlösung überein). Lass es ein kostenloses Mitglied sein k i i-ro-Gleichungen, also die Hauptvariable x i in der entsprechenden Grundlösung ist negativ.

Um zu einer neuen Basislösung überzugehen, müssen zwei Probleme gelöst werden:

1) legen Sie fest, welche nicht-Basisvariable in die Hauptvariable umgewandelt werden soll;

2) Wählen Sie eine Variable aus, die anstelle der Variablen, die aus den Hauptvariablen entfernt wurde, von den Hauptvariablen auf die Nicht-Basisvariablen übertragen werden soll.

Bei der Umwandlung einer Nicht-Basisvariablen in eine Hauptvariable nimmt sie nicht ab, sondern in der Regel zu: Anstelle von Null in der ursprünglichen Basislösung nimmt sie in der neuen Basislösung einen positiven Wert an (es gibt nur eine Ausnahme). im Falle einer Degeneration). Um die Frage zu lösen, welche Nicht-Basisvariablen in Basisvariablen umgewandelt werden können, müssen Sie daher in der Lage sein, Nicht-Basisvariablen zu finden, bei denen die Hauptvariable, die in der ursprünglichen Basislösung negativ ist, zunimmt. Kehren wir zur i-ten Gleichung des Systems zurück, in der der freie Term k i Negativ. Es zeigt, dass die Variable x i nimmt mit der Zunahme derjenigen nichtbasisvariablen zu, deren Koeffizienten in dieser Gleichung positiv sind. Daraus folgt, dass diejenigen nicht-Basisvariablen, die in der Gleichung eines Systems mit negativem freien Term positive Koeffizienten haben, in Basisvariablen umgewandelt werden können.

Drei Fälle mögen hier vorliegen.

1. In der i-ten Gleichung des Systems gibt es keine Nebenvariablen mit positiven Koeffizienten, also alle Koeffizienten b i, j sind negativ (wie auch der freie Term). k i). In diesem Fall ist dieses System der Beschränkungen inkonsistent – es gibt keine einzige zulässige Lösung. Aufgrund der Nichtnegativität aller Variablen, einschließlich x m + l ,...,x n , die i-te Gleichung, in der der freie Term k i und alle Koeffizienten b i , m + l ,...,b i , n negativ sind, folgt daraus, dass die Variable x i- kann keine nichtnegativen Werte annehmen. Wenn es jedoch keine einzige zulässige Lösung für ein System von Randbedingungen gibt, dann gibt es auch keine optimale Lösung.

2. Die i-te Gleichung hat eine Variable x t+ j, dessen Koeffizient positiv ist. In diesem Fall wird diese Variable auf die Hauptvariablen übertragen.

3. Die i-te Gleichung hat mehrere Variablen mit positiven Koeffizienten. In diesem Fall kann jeder von ihnen in Basisversionen umgewandelt werden.

Als nächstes müssen Sie festlegen, welche Hauptvariable in eine Nicht-Basisvariable konvertiert werden soll. Dazu sollten Sie die Regel verwenden: Ermitteln Sie die Verhältnisse der freien Terme zu den Koeffizienten der in die Hauptvariablen umzuwandelnden Variablen aus allen Gleichungen, bei denen die Vorzeichen der freien Terme und der angegebenen Koeffizienten entgegengesetzt sind, und berücksichtigen Sie dann die Absolutwert dieser Verhältnisse und wählen Sie das kleinste aus ihnen aus (wenn in einigen Gleichungen die Vorzeichen der freien Terme und Koeffizienten übereinstimmen oder in einigen Gleichungen keine Variable vorhanden ist, die in Basisvariablen umgewandelt werden kann, wird das Verhältnis als gleich ∞ betrachtet).

Die Gleichung, aus der sich das kleinste Verhältnis ergibt, wird isoliert. Die hervorgehobene Gleichung zeigt, welche der Hauptvariablen in Nichtbasisvariablen umgewandelt werden sollten. Nachdem sie die neuen Hauptvariablen durch nicht-grundlegende Variablen ausgedrückt haben, gehen sie zur nächsten Grundlösung über.

Das Ergebnis ist ein systemähnliches Gleichungssystem, bei dem die Anzahl der negativen freien Ahornbäume entweder mit ihrer Anzahl im System übereinstimmt oder um eins kleiner ist. Dies hängt davon ab, ob der Achsenabschnitt in der hervorgehobenen Gleichung positiv oder negativ ist.

Wenn der freie Term in der ausgewählten Gleichung negativ ist, ist die Anzahl der negativen Komponenten in der neuen Basislösung um eins geringer als in der ursprünglichen. Wenn in der gewählten Gleichung der freie Term positiv (oder gleich Null) ist, bleibt in der neuen Basislösung die Anzahl der negativen Komponenten dieselbe wie in der ursprünglichen.

Wir erhalten also eine neue, verbesserte Basislösung, die näher am Bereich der zulässigen Lösungen des Randbedingungssystems liegt. Wenn sich herausstellt, dass es nicht akzeptabel ist, sollte das gleiche Schema erneut angewendet werden. Als Ergebnis erhält man nach einer endlichen Anzahl von Schritten eine zulässige Grundlösung.

Fortsetzung von Beispiel 4.1. Wir müssen eine zulässige Grundlösung für dieses System von Einschränkungen finden, die die lineare Form maximiert.

Da das Zwangsbedingungssystem ein System aus vier unabhängigen Gleichungen mit sechs Variablen ist, sollte die Anzahl der Hauptvariablen vier und die Anzahl der Nichtgrundvariablen zwei betragen.

Um ein Problem mit der Simplex-Methode zu lösen, müssen Sie zunächst eine grundlegende Lösung finden. In diesem Fall ist es einfach. Dazu reicht es aus, zusätzliche Variablen als Hauptvariablen zu verwenden X 3 , X 4 , X 5 , X 6. Da die Koeffizienten dieser Variablen eine Identitätsmatrix bilden, ist die Berechnung der Determinante nicht erforderlich. Zählen von Nicht-Kernvariablen X 1 , X 2 gleich Null, erhalten wir die Grundlösung (0; 0; 120; 160; 120; 80), die sich ebenfalls als zulässig herausstellte. Daher ist es nicht erforderlich, die erste Stufe der Simplex-Methode anzuwenden.

Wir gehen direkt zur zweiten Stufe über, also zur Suche nach einer optimalen Lösung.

1 Schritt. Hauptvariablen: x 3, x 4, x 5, x 6; Nicht-Kernvariablen: X 1 , X 2. Im System drücken wir die Hauptvariablen durch nicht grundlegende Variablen aus. Um zu beurteilen, ob nicht-grundlegende Variablen unter den nicht-grundlegenden Variablen belassen werden sollten oder ob es im Hinblick auf die Annäherung an die optimale Lösung rentabler ist, sie auf die Hauptvariablen zu übertragen, ist es notwendig, eine lineare Form durch auszudrücken sie (in diesem Fall wird es bereits durch die Variablen ausgedrückt). X 1 , X 2) Dann erhalten wir:

Bei X 1 = X 2 = 0 haben wir X 3 = 120, X 4 = 160, X 5 = 120, X 6 = 80, was die Grundlösung (0; 0; 120; 160; 120; 80) ergibt, die wir als Ausgangspunkt genommen haben. Bei dieser Grundlösung ist der Wert der Linearform =0.

Als wir dachten X 1 = X 2 = 0 (Produktion produziert nichts), das Ziel wurde gesetzt – die erste, egal welche, Grundlösung zu finden. Dieses Ziel wurde erreicht. Jetzt müssen wir von dieser anfänglichen Lösung zu einer anderen übergehen, bei der der Wert der linearen Form zunimmt. Aus der Betrachtung der linearen Form wird deutlich, dass ihr Wert mit steigenden Werten der Variablen zunimmt X 1 und X 2. Mit anderen Worten, es ist unrentabel, diese Variablen als nicht-basisch zu betrachten, d.h. gleich Null, sie müssen in die Anzahl der Basisvariablen umgewandelt werden. Dies bedeutet einen Übergang zu einer neuen Basislösung. Bei der Simplex-Methode wird bei jedem Lösungsschritt davon ausgegangen, dass nur eine der freien Variablen in die Hauptvariable umgewandelt wird. Lassen Sie uns die Variable in die Anzahl der Basisvariablen umwandeln X 2, da es im Ausdruck der linearen Form mit einem großen Koeffizienten enthalten ist.

Sobald eine der freien Variablen zu einer der Hauptvariablen wird, muss an ihrer Stelle eine der Hauptvariablen in die Anzahl der Nicht-Basisvariablen übertragen werden. Welche der vier Hauptvariablen soll abgeleitet werden? Die folgenden Überlegungen helfen bei der Beantwortung dieser Frage.

Bedeutung X 2 muss so groß wie möglich gemacht werden, da dies dem Endziel entspricht – der Maximierung F. Es stellt sich jedoch heraus, dass der Anstieg X 2 kann nur bis zu bekannten Grenzen fortgesetzt werden, nämlich bis die Anforderung der Nichtnegativität von Variablen verletzt wird. Aus der ersten Gleichung des Systems folgt also, dass die Variable x 2 die Zahl 120/4 nicht überschreiten sollte, d.h. X 2 ≤30, da nur mit diesen Werten X 2 variabel X 3 bleibt positiv (falls X 2 = 30 also X 3 = 0; Wenn X 2 >30 also X 3 < 0). Из третьего уравнения системы следует, что X 2 ≤ 120/2, d.h. X 2 ≤ 60, ab dem vierten - was X 2 ≤ 80/2, d.h. X 2 ≤ 40 (in der zweiten Gleichung die Variable X 2 nicht im Lieferumfang enthalten). Erfüllt alle diese Bedingungen X 2 ≤ 30.

Mit anderen Worten: Um die Frage zu beantworten, welche Variable in eine Nicht-Basisvariable umgewandelt werden soll, müssen Sie akzeptieren X 2 = min (120/4; 120/2; 80/2) = min (30; 60; 40) = 30. Dann X 3 = 0 und X 3 wird eine nicht-primäre Variable und x 4 und x 5 bleiben positiv,

Schritt 2. Schlüsselvariablen: X 2 , X 4 , X 5 , X 6 Nebenvariablen: X 1 und X 3. Lassen Sie uns die Hauptvariablen und die lineare Form durch nicht-grundlegende Variablen ausdrücken. Im System nehmen wir die Gleichung, aus der der Mindestwert des Verhältnisses des freien Termes zum Koeffizienten bei stammt X 2. In diesem Fall handelt es sich um die erste Gleichung. Aus dieser Gleichung ausgedrückt X 2, wir haben, X 2 = 30 - 0,25 · X 3. Ersetzen wir diesen Ausdruck X 2 in alle anderen Gleichungen des Systems (4.4) und in lineare Form F und wenn wir ähnliche Begriffe bringen, erhalten wir

Bei X 1 = X 3 = 0 haben wir F= 90. Das ist schon besser als bei Schritt 1, aber nicht das gewünschte Maximum. Weitere Funktionssteigerung F möglich durch Einführung einer Variablen X 1 unter den wichtigsten; da diese Variable im Ausdruck enthalten ist F mit einem positiven Koeffizienten führt sein Anstieg daher zu einem Anstieg der linearen Form und es ist unrentabel, ihn als nichtbasisch zu betrachten, d.h. gleich Null.

Um die Frage zu beantworten, welche Variable von den Hauptvariablen auf die Nichtgrundvariablen abgeleitet werden soll, akzeptieren wir X 1 = min (160/4; 60/2; 20/1) = 20. Dann X 6 = 0 und X 6 wird eine Nicht-Hauptvariable und X 4 und X 5 bleiben positiv.

Die erste Gleichung wird bei der Ermittlung des angegebenen Minimums nicht verwendet, da X] ist in dieser Gleichung nicht enthalten.

Schritt 3. Schlüsselvariablen: X 1 , x 2 , x 4 , x 5; Nebenvariablen: x 3, x 6. Lassen Sie uns die Hauptvariablen und die lineare Form durch nicht-grundlegende Variablen ausdrücken. Aus der letzten Gleichung des Systems (4.5) (sie ist hervorgehoben) haben wir X 1 = 20 + 0,5 · X 3 - X 6. Wenn wir diesen Ausdruck in die übrigen Gleichungen und in die lineare Form einsetzen, erhalten wir

Aus dem Ausdruck der linearen Form folgt, dass ihr Maximalwert noch nicht erreicht wurde, da eine Steigerung möglich ist F durch Einführung in die Hauptvariable X 3 (es hat einen positiven Koeffizienten). Wir glauben X 3 = min (∞; 30/0,25; 80/2; 20/0,5) =40.

Hier stoßen wir zunächst auf zwei Regelungen, die einer weiteren Klarstellung bedürfen.

Erstens, obwohl die Variable X 3 und ist im Ausdruck für enthalten X 1 (die erste Gleichung des Systems (4.6), hat aber einen positiven Koeffizienten für jede Erhöhung X 3 variabel X 1 kann nicht negativ werden. Mit anderen Worten: In der ersten Gleichung gibt es keine Einschränkungen hinsichtlich der Vergrößerung der Variablen X 3 überschneidet sich nicht, daher schreiben wir herkömmlicherweise ∞. In Zukunft werden wir uns darauf einigen, dieselbe Notation zu verwenden, wenn die neu in die Liste der Grundvariablen aufgenommene Variable in keiner Gleichung des Zwangssystems enthalten ist.

Zweitens erhalten wir zwei identische Mindestwerte gleich 40. Wenn X 3 = 40 also X 4 = 0 und x 5 = 0, d.h. die Schlussfolgerung liegt nahe, dass anstelle einer Variablen zwei gleichzeitig auf die Zahl der Nicht-Basisvariablen übertragen werden sollten: X 4 und x 5. Die Anzahl der Hauptvariablen sollte jedoch nicht weniger als vier betragen. Gehen Sie dazu wie folgt vor. Eine der Variablen ( X 4 oder X 5.) bleibt unter den Basislösungen, ihr Wert wird jedoch als gleich Null betrachtet, d. h. die im nächsten Schritt erhaltene Basislösung erweist sich als entartet. Lass uns zum Beispiel gehen, X 4 unter den Hauptvariablen und X 5 werden auf die Anzahl der nicht zum Kerngeschäft gehörenden übertragen.

Schritt 4 Schlüsselvariablen: X 1, x 2, X 3 , X 4 ; Nicht-Hauptvariablen: x 5, x 6. Lassen Sie uns die Hauptvariablen und die lineare Form ausdrücken F durch nicht-primäre, wobei dieser Ausdruck mit der vierten Gleichung des Systems (4.6) beginnt. Als Ergebnis erhalten wir

Da im Ausdruck eine lineare Form der Variablen vorliegt X 5 und X 6 mit negativen Koeffizienten eingeben, dann keine Erhöhung F aufgrund dieser Variablen ist unmöglich.

Das Fehlen von Nebenvariablen mit positiven Koeffizienten in einem Schritt der Simplex-Methode im Ausdruck der linearen Form F, deren Maximum gesucht wird, ist ein Optimalitätskriterium.

Folglich ist in Schritt 4 das Optimalitätskriterium erreicht und das Problem gelöst. Die optimale Lösung ist (40; 20; 40; 0; 0; 0), wobei F max =140. Um den größten Gewinn zu erzielen, beträgt der Betrag 140 Höhlen. Einheiten, aus diesen Ressourcen müssen 40 Produktionseinheiten aus Heufeldern und 20 aus Ackerland gewonnen werden. In diesem Fall werden die Ressourcen der Typen II, III und IV vollständig und 40 Einheiten genutzt. Typ I bleibt unverbraucht.

Beispiel 4.2. Finden Sie das Maximum einer Funktion F=x 1 + 2 X 2 mit Einschränkungen

Wir führen zusätzliche nichtnegative Variablen ein X 3 ,X 4 ,X 5 ,X 6 und reduzieren Sie dieses Ungleichungssystem auf sein äquivalentes Gleichungssystem

Als Hauptvariablen nehmen wir die eingeführten Zusatzvariablen, da in diesem Fall die Grundlösung des Systems leicht zu finden ist. Dann X 1 und X 2 - Nebenvariablen.

1 Schritt. Schlüsselvariablen: X 3 ,X 4 , X 5 , X 6; Nicht-Kernvariablen; X 1 und X 2. Wenn wir die Hauptvariablen durch nicht-grundlegende Variablen ausdrücken, erhalten wir

Folglich entspricht diese Aufteilung der Variablen in Basis und Nicht-Basis der Basislösung (0; 0; - 2; - 4; 2; 6), die inakzeptabel ist (zwei Variablen sind negativ) und daher nicht optimal. Von dieser Grundlösung werden wir zu einer verbesserten Lösung übergehen.

Um zu entscheiden, welche Variable von der Nebenvariable zur Grundvariable übertragen werden soll, betrachten Sie eine der beiden verfügbaren Gleichungen des letzteren Systems mit negativen freien Termen, beispielsweise die zweite. Es zeigt, dass eine Übersetzung in Basisvariablen möglich ist X 1 und X 2, da sie in dieser Gleichung positive Koeffizienten haben (was passiert also, wenn sie zunehmen, wenn wir eine von ihnen in die Hauptvariablen, die Variable, übersetzen? X 4 erhöht sich).

Versuchen wir es in die Hauptvariable zu übersetzen X 1 . Um festzustellen, welche Variable von der Basis zur Nichtbasis übertragen werden soll, ermitteln wir den Absolutwert des kleinsten Verhältnisses der freien Terme des Systems zu den Koeffizienten bei X 1 , wir haben X 1 = min (∞; 4/1; 2/1; ∞) = 2. Es ergibt sich aus der dritten Gleichung und zeigt, dass die Variable in Nebenvariablen umgewandelt werden muss X 5, was in der ursprünglichen Basislösung positiv ist.

Folglich enthält die resultierende Basislösung wie die ursprüngliche zwei negative Komponenten, d. h. beim Übergang zu einer solchen Basislösung wird es keine Verbesserung geben.

Wenn wir in die Hauptvariable übersetzen X 2 , dann das kleinste Verhältnis von freien Termen zu Koeffizienten bei X 2 wird sein X 2 - min (2/2; 4/1; ∞; 6/1) = 1. Es ergibt sich aus der ersten Gleichung, in der der freie Term negativ ist. Deshalb übersetzen X 2 in den wichtigsten, und X 3 in Nebenvariablen zerlegen, erhalten wir eine Grundlösung, bei der die Anzahl der negativen Komponenten um eins geringer ist als im Original. Konzentrieren wir uns daher auf diese Möglichkeit: Wir übersetzen X 2 in den wichtigsten, und X 3 in Nicht-Hauptvariablen; dann wird die erste Gleichung hervorgehoben.

Schritt 2. Schlüsselvariablen: X 2 ,X 4 ,X 5 ,X 6; Nicht-Kernvariablen: X 1 und X 3. Lassen Sie uns die neuen Hauptvariablen durch die neuen nicht-grundlegenden Variablen ausdrücken, beginnend mit der in Schritt 1 hervorgehobenen Gleichung. Als Ergebnis erhalten wir

Folglich haben wir eine neue Grundlösung (0; 1; 0; -3; 3; 5), die ebenfalls ungültig und daher nicht optimal ist. Aber wie wir vorhergesagt haben, ist darin nur eine Variable negativ (nämlich X 4).

Von der erhaltenen Grundlösung ist es notwendig, zu einer anderen überzugehen. Betrachten wir eine Gleichung mit einem negativen freien Term, d.h. zweite Gleichung. Es zeigt, dass eine Übersetzung in Basisvariablen möglich ist X 1 und X 3. Lassen Sie uns in Hauptvariablen konvertieren X 1 . Finden wir den kleinsten der absoluten Werte der Verhältnisse der freien Terme des Systems zu den Koeffizienten bei X 1 ; wir haben X 1 = min (∞; 3/1,5; 3/0,5; 5/0,5) = 2. Das bedeutet, dass wir umrechnen müssen X 4 . Da sich aus der zweiten Gleichung das kleinste Verhältnis ergibt, isolieren wir es. Die neue Grundlösung enthält keine negativen Bestandteile mehr, ist also zulässig.

Schritt 3. Schlüsselvariablen: X 1 , X 2 , X 5 , X 6; Nicht-Kernvariablen: X 3 , X 4 . Wenn wir die Hauptvariablen durch nicht-grundlegende Variablen ausdrücken, erhalten wir

Die neue Grundlösung hat die Form (2; 2; 0; 0; 2; 4). Ob sie optimal ist, lässt sich ermitteln, indem man eine lineare Form anhand der Nebenvariablen der betrachteten Grundlösung ausdrückt. Nachdem wir dies getan haben, erhalten wir . Daher greifen wir nur dann auf die lineare Form zurück, wenn die Grundlösung realisierbar ist. Da wir das Maximum einer linearen Form suchen, ist die resultierende Grundlösung nicht optimal.

Umrechnen der Anzahl der Hauptvariablen X 4 mit einem größeren positiven Koeffizienten.

Wir finden X 4 = min (∞; ∞; 2: (1/3); 4/(1/3)) = 6. Dieses kleinste Verhältnis ergibt sich aus der dritten Gleichung des Systems, die wir auswählen. Es zeigt das wann X 4 =6 variabel X 5 = 0 und wird daher nicht primär.

Schritt 4 Schlüsselvariablen: X 1 , X 2 , X 4 , X 6;Nebenvariablen: X 3 , X 5 . Wenn wir die Hauptvariablen durch nicht-grundlegende Variablen ausdrücken, erhalten wir

Die lineare Form, ausgedrückt durch dieselben nicht-Basisvariablen, wird die Form annehmen. Daher ist die Grundlösung (6; 4; 0; 6; 0; 2), zu der wir übergegangen sind, nicht optimal.

Eine Erhöhung der linearen Form ist beim Übergang zu einer neuen Grundlösung möglich, bei der die Variable x 3 die Hauptvariable ist. Wir finden X 3 = min (∞; ∞; co; 2/1) = 2. Dieses kleinste Verhältnis ergibt sich aus der vierten Gleichung des Systems und zeigt, wann X 3 = 2 Variable X 6 = 0 und wird nicht primär.

Schritt 5 Schlüsselvariablen: X 1 , X 2 , X 3 , X 4 Nebenvariablen X 5 ,X 6. Wenn wir die Hauptvariablen durch nicht-grundlegende Variablen ausdrücken, erhalten wir

Die lineare Form, ausgedrückt durch die Nebenvariablen der neuen Grundlösung, hat die Form . Das Optimalitätskriterium für den Fall der linearen Formmaximierung ist erfüllt. Daher ist die Grundlösung (8; 6; 2; 10, 0; 0) optimal und das Maximum der linearen Form F max = 20.

4.5 Grafische Problemlösung

Lineares Programmieren

Es empfiehlt sich, eine grafische Methode zur Lösung linearer Programmierprobleme zu verwenden für:

Lösungen für Probleme mit zwei Variablen, wenn Einschränkungen durch Ungleichungen ausgedrückt werden;

Lösungen für Probleme mit vielen Variablen, sofern deren kanonische Notation nicht mehr als zwei freie Variablen enthält.

Schreiben wir ein lineares Programmierproblem mit zwei Variablen:

Zielfunktion:

Einschränkungen:

Jede der Ungleichungen (4.8) des Zwangssystems des Problems definiert geometrisch jeweils eine Halbebene mit Grenzgeraden; . Wenn das Ungleichungssystem (4.8) konsistent ist, ist der Bereich seiner Lösungen die Menge der Punkte, die zu allen angegebenen Halbebenen gehören. Da die Menge der Schnittpunkte dieser Halbebenen konvex ist, ist der Bereich möglicher Lösungen eine konvexe Menge, die als Lösungspolygon bezeichnet wird. Die Seiten dieses Polygons liegen auf Geraden, deren Gleichungen aus dem ursprünglichen Zwangssystem durch Ersetzen von Ungleichheitszeichen durch Gleichheitszeichen erhalten werden.

Der Bereich zulässiger Lösungen des Ungleichungssystems (4.8) kann sein:

Konvexes Polygon;

Konvexer, polygonaler, unbegrenzter Bereich;

Leerer Bereich;

Liniensegment;

Der einzige Punkt.

Die Zielfunktion (4.7) definiert eine Familie paralleler Linien auf der Ebene, von denen jede einem bestimmten Z-Wert entspricht.

Ein Vektor mit den Koordinaten und , senkrecht zu diesen Linien, gibt die Richtung des schnellsten Anstiegs von Z an, und der entgegengesetzte Vektor gibt die Richtung der Abnahme von Z an.

Wenn wir den Bereich zulässiger Lösungen des Ungleichungssystems (4.8) und der Familie paralleler Geraden (4.7) im selben Koordinatensystem darstellen, reduziert sich das Problem der Bestimmung des Maximums der Funktion Z auf die Suche nach dem zulässigen Region der Punkt, durch den eine Linie aus der Familie Z = const verläuft und der dem größten Wert des Z-Parameters entspricht.

Dieser Punkt existiert, wenn das Lösungspolygon nicht leer ist und die Zielfunktion darauf nach oben begrenzt ist. Unter den angegebenen Bedingungen nimmt die Zielfunktion an einem der Eckpunkte des Lösungspolygons den Maximalwert an.

Um diesen Scheitelpunkt zu bestimmen, konstruieren wir eine Höhenlinie, die durch den Koordinatenursprung und senkrecht zum Vektor verläuft, und verschieben sie in Richtung des Vektors, bis sie den letzten Extrempunkt (Eckpunkt) des Lösungspolygons berührt. Die Koordinaten des angegebenen Punktes bestimmen den optimalen Plan für diese Aufgabe.

Abbildung 4.1 – Das Optimum der Funktion Z ist am Punkt A erreichbar

Abbildung 4.2 – Die optimale Funktion Z wird an jedem Punkt erreicht [AB]

Zum Abschluss unserer Betrachtung der geometrischen Interpretation des Problems (4.7) – (4.8) stellen wir fest, dass bei der Lösungsfindung die in Abb. 4.1 - 4.4. Abbildung 4.1 charakterisiert den Fall, dass die Zielfunktion ihren Maximalwert an einem einzelnen Punkt A annimmt. Aus Abbildung 4.2 wird deutlich, dass die Zielfunktion an jedem Punkt der Strecke AB ihren Maximalwert annimmt.

Abbildung 4.3 – Die optimale Funktion Z ist unerreichbar

Abbildung 4.4 – Bereich möglicher Lösungen – leerer Bereich

Abbildung 4.3 zeigt den Fall, in dem das Maximum unerreichbar ist, und Abbildung 4.4 zeigt den Fall, in dem das Randbedingungssystem des Problems inkonsistent ist. Beachten Sie, dass sich die Ermittlung des Minimalwerts von Z unter einem gegebenen Restriktionssystem von der Ermittlung seines Maximalwerts unter denselben Einschränkungen nur dadurch unterscheidet, dass sich die Z-Ebenenlinie nicht in Richtung des Vektors, sondern in die entgegengesetzte Richtung bewegt. Somit treten die oben genannten Fälle, die beim Ermitteln des Maximalwerts der Zielfunktion auftreten, auch bei der Bestimmung ihres Minimalwerts auf.

Um das lineare Programmierproblem (4.7) – (4.8) auf der Grundlage seiner geometrischen Interpretation praktisch zu lösen, ist Folgendes erforderlich.

1. Konstruieren Sie Geraden, deren Gleichungen durch Ersetzen der Ungleichheitszeichen in den Einschränkungen (4.4) durch Gleichheitszeichen erhalten werden.

2. Finden Sie die Halbebenen, die durch jede der Randbedingungen des Problems definiert werden.

3.Definieren Sie das Lösungspolygon.

4. Konstruieren Sie einen Vektor.

5. Konstruieren Sie eine gerade Linie, die durch den Koordinatenursprung und senkrecht zum Vektor verläuft.

6. Bewegen Sie die Gerade in Richtung des Vektors, wodurch sie entweder den Punkt (die Punkte) finden, an dem die Zielfunktion den Maximalwert annimmt, oder die Unbegrenztheit der Funktion von oben auf der Menge der Pläne feststellen .

7. Bestimmen Sie die Koordinaten des Maximalpunkts der Funktion und berechnen Sie den Wert der Zielfunktion an diesem Punkt.

Beispiel 4.3. Das Unternehmen produziert zwei Arten von Produkten P und R, die im Großhandel verkauft werden. Für die Herstellung von Produkten werden zwei Arten von Rohstoffen A und B verwendet. Die maximal möglichen Rohstoffvorräte pro Tag betragen 9 bzw. 13 Einheiten. Der Verbrauch an Rohstoffen des Typs A für die Herstellung der Produkte P und P beträgt 2 bzw. 3 Einheiten, des Typs B - 3 bzw. 2 Einheiten. Erfahrungsgemäß übersteigt die tägliche Nachfrage nach Produkt P die Nachfrage nach Produkt P nie um mehr als 1 Einheit. Darüber hinaus ist bekannt, dass die Nachfrage nach Produkt P nie mehr als 2 Einheiten pro Tag beträgt. Die Großhandelspreise pro Produktionseinheit betragen 3 Einheiten für P und 4 Einheiten für P. Wie viel von jedem Produkttyp sollte das Unternehmen produzieren, damit die Verkaufserlöse maximiert werden? Lösen Sie das Problem mit einer geometrischen Methode.

Lösung. Konstruieren wir ein Lösungspolygon (Abb. 7.5). Dazu zeichnen wir im Koordinatensystem X 1 OX 2 auf der Ebene die Grenzlinien:

Anhand eines beliebigen Punktes, zum Beispiel des Ursprungs, bestimmen wir, welche Halbebene die entsprechende Ungleichung definiert. Durch Ungleichungen definierte Halbebenen in Abb. 7.5 sind durch Pfeile dargestellt. Der Lösungsbereich ist das Polygon OABCD.

Um eine gerade Linie zu konstruieren, konstruieren wir einen Gradientenvektor und zeichnen durch den Punkt 0 eine gerade Linie senkrecht dazu. Wir verschieben die konstruierte Gerade Z= 0 parallel zu sich selbst in Richtung des Vektors. Aus Abbildung 4.5 folgt, dass diese Linie in Bezug auf das Lösungspolygon im Punkt C zur Referenzlinie wird, wo die Funktion ihren Maximalwert annimmt. Punkt C liegt am Schnittpunkt der Linien L 1 und Z 3. Um seine Koordinaten zu bestimmen, lösen wir das Gleichungssystem:

Optimaler Aufgabenplan = 2,4; =1,4. Wenn wir die Werte und in die lineare Funktion einsetzen, erhalten wir:

3 2,4 + 4 1,4 = 12,8.

Die resultierende Lösung bedeutet, dass das Produktionsvolumen von Produkt P 2,4 Einheiten und von Produkt P 1,4 Einheiten betragen sollte. Das erhaltene Einkommen beträgt in diesem Fall: Z = 12,8 cu.

Abbildung 4.5 – Lösen eines linearen Programmierproblems mit einer geometrischen Methode

5. DOPPELTE PROBLEME

Zusammensetzung eines dualen Problems. Betrachten Sie zwei lineare Programmierprobleme:

Funktion maximieren

unter Einschränkungen

Funktion minimieren

unter Einschränkungen

Diese Aufgaben haben die folgenden Eigenschaften:

1. In einem Problem wird das Maximum einer linearen Form gesucht, in dem anderen das Minimum.

2°. Koeffizienten von Variablen in der linearen Form eines Problems sind freie Mitglieder des Zwangssystems eines anderen Problems; im Gegenteil sind freie Mitglieder des Zwangssystems eines Problems Koeffizienten von Variablen in der linearen Form eines anderen Problems.

3°. In jedem Problem wird ein System von Einschränkungen in Form von Ungleichungen angegeben, und sie haben alle die gleiche Bedeutung, nämlich: Wenn das Maximum einer linearen Form gefunden wird, haben diese Ungleichungen die Form, und wenn sie das Minimum finden, haben sie die bilden

4°. Koeffizienten von Variablen in Zwangssystemen werden durch Matrizen beschrieben

die relativ zueinander vertauscht sind.

5°. Die Anzahl der Ungleichungen im Randsystem eines Problems stimmt mit der Anzahl der Variablen eines anderen Problems überein.

6 f. Die Bedingungen für die Nichtnegativität von Variablen bleiben in beiden Problemen erhalten.

Zwei lineare Programmierprobleme, die die oben genannten Bedingungen erfüllen, werden als symmetrische duale Probleme bezeichnet. Wir werden nur symmetrische duale Probleme untersuchen und sie daher kurz als duale Probleme bezeichnen.

Somit kann jedem linearen Programmierproblem sein duales Problem zugeordnet werden. Wir nennen das ursprüngliche Problem das ursprüngliche (oder direkte) Problem. Das direkte Problem und sein duales Problem bilden zusammengenommen ein Paar gegenseitig dualer Probleme, und jedes von ihnen kann als das ursprüngliche Problem betrachtet werden, dann wird das andere dazu dual sein.

Aus dem oben Gesagten ergeben sich die folgenden Regeln zum Verfassen eines Problems, das dual zum ursprünglichen Problem ist:

1. Alle Ungleichungen im Zwangssystem des ursprünglichen Problems werden auf Ungleichungen gleicher Bedeutung reduziert: Wenn im ursprünglichen Problem das Maximum einer linearen Form gesucht wird, auf die Form ≤, wenn das Minimum, auf die Form ≥. Hierzu werden Ungleichungen, bei denen diese Voraussetzung nicht erfüllt ist, mit - 1 multipliziert.

2. Schreiben Sie die Matrix A der Koeffizienten für die Variablen des ursprünglichen Problems auf, die Sie nach der Transformation von Schritt 1 erhalten, und erstellen Sie die Matrix A", transponiert in Bezug auf die Matrix A.

3. Erstellen Sie ein Restriktionssystem für das duale Problem, indem Sie die Elemente der Matrix A als Koeffizienten für die Variablen und die Koeffizienten für die Variablen in der linearen Form des ursprünglichen Problems als freie Terme nehmen und Ungleichungen des Gegenteils aufschreiben Bedeutung im Vergleich zu den in Schritt 1 erhaltenen Ungleichungen.

4. Erstellen Sie eine lineare Form des dualen Problems, indem Sie die freien Terme des in Schritt 1 erhaltenen Randbedingungssystems des ursprünglichen Problems als Koeffizienten für die Variablen verwenden.

5. Geben Sie an, was bei der Lösung eines dualen Problems gefunden werden muss, nämlich: ein Minimum einer linearen Form, wenn im ursprünglichen Problem ein Maximum gesucht wird, und ein Maximum, wenn im ursprünglichen Problem ein Minimum gesucht wird.

6. Schreiben Sie die Bedingung für die Nichtnegativität der Variablen des dualen Problems auf.

Beispiel 5.1. Erstellen Sie ein duales Problem wie folgt: Finden Sie das Maximum einer Funktion unter den Einschränkungen

Die dritte Ungleichung des Systems (*) erfüllt nicht Klausel 1 der Regeln zum Erstellen eines dualen Problems. Also multiplizieren wir es mit –1:

Um die Vorbereitung eines dualen Problems zu erleichtern, ist es besser, die erweiterte Matrix B zu verwenden, in der wir neben den Koeffizienten für die Variablen des Zwangssystems des ursprünglichen Problems auch die freien Terme und Koeffizienten für die Variablen aufschreiben in linearer Form, wobei zu diesem Zweck eine zusätzliche Spalte und Zeile hervorgehoben wird. Wir transponieren die Matrix B und erstellen mit der transponierten Matrix B / ein zu diesem duales Problem.

Das duale Problem reduziert sich darauf, das Minimum einer Funktion unter den Nebenbedingungen zu finden

Grundlegende Dualitätssätze

Die Theorie der Dualität in der linearen Programmierung basiert auf den folgenden Grundsätzen.

Satz 1. Wenn eines der linearen Programmierprobleme ein endliches Optimum hat, dann hat auch sein Dual ein endliches Optimum und die optimalen Werte der linearen Formen beider Probleme fallen zusammen, d.h. F max = Zmin oder Fmin = Zmax. Wenn die lineare Form eines der dualen Probleme nicht eingeschränkt ist, dann sind die Bedingungen des anderen Problems widersprüchlich.

Bevor wir den nächsten Satz formulieren, stellen wir Entsprechungen zwischen den Variablen im ursprünglichen und dualen Problem her.

Bei der Lösung des ursprünglichen Problems mit der Simplex-Methode ist es zur Reduzierung des Ungleichungssystems auf sein äquivalentes Gleichungssystem erforderlich, m zusätzliche nichtnegative Variablen einzuführen (entsprechend der Anzahl der Ungleichungen im Zwangssystem), wobei i = 1, 2,…,t bedeutet die Zahl der Ungleichung, in die die zusätzliche Variable eingeführt wurde.

Das Nebenbedingungssystem des dualen Problems besteht aus n Ungleichungen mit m Variablen. Wenn Sie dieses Problem mit der Simplex-Methode lösen, sollten Sie n zusätzliche nichtnegative Variablen einführen, wobei j = 1, 2,...,m die Nummer des Ungleichheitssystems von Nebenbedingungen des dualen Problems bedeutet, in das die zusätzliche Variable eingefügt wird wurde vorgestellt.

Stellen wir die folgende Entsprechung zwischen den Variablen im ursprünglichen und dualen Problem her:

Mit anderen Worten, jede Anfangsvariable
Problem x j (j = 1,2,…, n) ist mit der zusätzlichen Variablen verknüpft, die in die j - e-Ungleichung des dualen Problems eingeführt wurde, und jede zusätzliche Variable des ursprünglichen Problems (i = 1,2,…, t), eingeführt in ich- Die Ungleichung des ursprünglichen Problems ist die ursprüngliche Variable des dualen Problems.

Satz 2 . Die Komponenten der optimalen Lösung eines der Probleme (direkt oder dual) sind gleich den Absolutwerten der Koeffizienten für die entsprechenden Variablen im Ausdruck der linearen Form des anderen Problems (dual oder direkt), wenn es erreicht wird sein Optimum und vorausgesetzt, dass die resultierende optimale Lösung nicht degeneriert ist.

Aus den Sätzen 1 und 2 folgt: Wenn Sie eines der gegenseitig dualen Probleme lösen, also seine optimale Lösung und das Optimum der linearen Form finden, können Sie die optimale Lösung und das Optimum der linearen Form des aufschreiben anderes Problem.

Beispiel 5.2. Verwenden Sie die Simplex-Methode, um die im vorherigen Beispiel angegebenen direkten und dualen Probleme zu lösen.

Lösung eines direkten Problems. Reduzieren wir das System der Ungleichheitsbeschränkungen (siehe S. 268) auf ein Gleichungssystem, indem wir nichtnegative zusätzliche Variablen einführen:

Wir werden im ersten Schritt der Lösung die zusätzlichen Variablen x 3, x 4, x 5, x 6 als Hauptvariablen verwenden.

1 Schritt. Hauptvariablen: x 3, x 4, x 5, x 6; Nicht-Hauptvariablen: x 1, x 2. Lassen Sie uns die Hauptvariablen in Form von Nichtbasisvariablen ausdrücken (die lineare Form berücksichtigen wir in diesem Lösungsschritt nicht, da die entsprechende Basislösung nicht zulässig ist):

Um eine zulässige Basislösung zu erhalten, transformieren wir die Variable in Basislösungen. Wir finden = min (2/1; ∞; 1/1; 5/1) = 1. In diesem Fall die Variable x 5 geht in Nicht-Kern.

Schritt 2. Hauptvariablen: x 1, x 3, x 4, x 6 Nicht-Hauptvariablen; x 2, x 5. Lassen Sie uns die Hauptvariablen und die lineare Form durch nicht grundlegende Variablen ausdrücken:

Konvertieren wir es in die Hauptvariable x 5. Glauben x 5=min (∞; 1/1; ∞; 4/1) = 1, daraus schließen wir, dass die Variable x 3 in eine nicht-primäre Variable umgewandelt werden muss.

Schritt 3. Hauptvariablen: x 1, X 4, x 5, x 6, Nebenvariablen x 3, x 2. Wir haben

Die Variable x 2 wird in Basis umgewandelt. Finden Sie x 2 = min (∞; ∞;∞; 1/1)=1. Dann wird die Variable x 6 nicht primär.

Schritt 4. Hauptvariablen: x 1, x 2, X 4, x 5, ; Nicht-Hauptvariablen: x 2, x 6. Wir haben

Das Optimalitätskriterium ist erfüllt. Die optimale Lösung hat die Form (4; 1; 0; 5; 4; 0); mit dieser Lösung ist F max = 13.

Fortsetzung von Beispiel 5.1. Wir reduzieren das Nebenbedingungssystem des dualen Problems auf das Gleichungssystem:

Wir werden die zusätzlichen Variablen y 5 y 6 als Hauptvariablen im 1. Schritt der Lösung nehmen.

1 Schritt. Hauptvariablen: J 5, J 6; Nebenvariablen: y 1, y 2, y 3, y 4. Lassen Sie uns die Hauptvariablen durch nicht grundlegende Variablen ausdrücken:

Konvertieren wir y in die Hauptvariable 4. Wir finden y 4 = mm (3/1: 1/1 = 1. Die Variable y 6 geht in Nebeneinen.

Schritt 2. Hauptvariablen: J 4, J 5 Nebenvariablen: J 1, J 2, J 3, J 6. Wir haben

Lassen Sie uns die Variable y 1 in die Hauptvariablen umwandeln. Da y 1 = min (∞; 2/3) = 2/3, wird die Variable y 5 nichtprimär.

Schritt 3. Hauptvariablen y 1, y 4, Nebenvariablen: y 2, y 3, y 5, y 6. Da die entsprechende Grundlösung des Problems zulässig ist, drücken wir nicht nur die Hauptlösungen in Form von Nicht-Basisvariablen aus, sondern auch in linearer Form:

Das Optimalitätskriterium (für den Fall der Minimierung einer linearen Form) ist erfüllt. Die optimale Lösung hat die Form (2/3; 0; 0; 7/3; 0; 0), mit Z min = 13.

Nachdem wir das duale Problem gelöst haben, sind wir von der Gültigkeit des ersten Teils von Satz 1 überzeugt: Das duale Problem hat auch ein endgültiges Optimum und Z min = =F max = 13.

Stellen wir sicher, dass auch die Aussage von Satz 2 wahr ist. Dazu schreiben wir die Variablen des direkten und des dualen Problems auf und behalten ihre Entsprechung bei;

Lassen Sie uns die im letzten Schritt der Lösung des dualen Problems erhaltene lineare Form anhand aller Variablen dieses Problems ausdrücken:

Betrachten Sie die Koeffizienten der Variablen y j in dieser linearen Form und berücksichtigen Sie ihre Entsprechung mit den Koeffizienten der Variablen xi, wir erhalten eine Lösung (4; 1; 0; 5; 4; 0), die mit der optimalen Lösung des direkten Problems übereinstimmt.

Kommentar. Nachdem Sie das direkte Problem gelöst haben, können Sie sofort eine Lösung für das duale Problem erhalten. Wenn wir die im 4. Schritt der Lösung des direkten Problems erhaltene lineare Form F durch alle Variablen dieses Problems ausdrücken, erhalten wir

Basierend auf Satz 2 finden wir unter Berücksichtigung der Entsprechung zwischen den Variablen im direkten und dualen Problem und unter Berücksichtigung des Absolutwerts der Koeffizienten der Variablen die optimale Lösung für das duale Problem (2/3; 0; 0; 7). /3; 0; 0). In diesem Fall ist Z min =F max = 13.

6 TRANSPORTPROBLEM

Dieser Fall entspricht dem gegenseitigen Widerspruch der im Problem enthaltenen Einschränkungen.

2) Die zulässige Menge ist ein konvex beschränktes Polyeder.

Eine zulässige Menge ist eine konvexe unbeschränkte Polyedermenge.

Die letzten beiden Fälle kann man sich zwei- oder dreidimensional recht gut vorstellen. In einem höherdimensionalen Raum wird das Konzept eines Polyeders (polyedrischer Menge) abstrakt als Schnittpunkt von Hyperebenen und Hyperhalbebenen eingeführt, die durch die entsprechenden linearen Gleichungen und Ungleichungen definiert werden, die in den Randbedingungen des Problems enthalten sind. Eine charakteristische Eigenschaft eines Polyeders ist das Vorhandensein singulärer Punkte darin - Gipfel.

Mögliche Fälle optimaler Lösungen (Pläne) für ein lineares Programmierproblem.

1) Problem hat keine optimalen Lösungen.

Dieser Fall kann auftreten: Entweder wenn die zulässige Lösungsmenge leer ist („es gibt nichts zur Auswahl“ der optimale Plan),

oder wenn die zulässige Menge eine unbeschränkte polyedrische Menge ist und die Zielfunktion darauf ins Unendliche wächst (wenn L max) oder nimmt unbegrenzt ab (mit Lmin).

2) Die Aufgabe hat Das einzige Lösung(der einzig optimale Plan).

Diese Lösung fällt notwendigerweise mit einem der Eckpunkte der zulässigen Menge zusammen.

3) Die Aufgabe hat unendliche Menge optimale Lösungen, gegeben durch eine lineare Formation – eine Kante, eine Fläche, eine Hyperfläche usw. Zu den Punkten dieser Linienformation gehören auch Eckpunkte der zulässigen Menge.

Somit lässt sich die Hauptaussage der Theorie der linearen Programmierung, die letztlich die konkreten Lösungswege bestimmt, wie folgt formulieren:

Wenn ein lineares Programmierproblem mindestens einen optimalen Plan hat, sollte dieser unter den Eckpunkten der zulässigen Lösungsmenge gesucht werden.

Im nächsten Abschnitt werden die diskutierten allgemeinen Prinzipien am Beispiel eines linearen Programmierproblems mit zwei Variablen veranschaulicht.

Grafisch-analytische Methode zur Lösung linearer Programmierprobleme

Die graphoanalytische (grafische) Methode zur Lösung linearer Programmierprobleme wird üblicherweise zur Lösung von Problemen mit zwei Variablen verwendet, bei denen die Einschränkungen durch Ungleichungen ausgedrückt werden, sowie von Problemen, die auf solche Probleme reduziert werden können.

Das lineare Programmierproblem habe die Form:

(1.7)

Wo Mit 1 , Mit 2 , A ich 1, A ich 2, B i - gegebene reelle Zahlen; die Vorzeichen in den Ungleichungen sind willkürlich; Die Zielfunktion wird entweder maximiert oder minimiert.

Jede der Ungleichungen (1.7) des Zwangssystems des Problems definiert geometrisch jeweils die Halbebene mit den Grenzgeraden
;ich=1,…,M. Wenn das Ungleichungssystem (1.7) konsistent ist, ist der zulässige Lösungsbereich des Problems die Menge der Punkte, die zu allen angegebenen Halbebenen gehören. Da die Menge der Schnittpunkte dieser Halbebenen konvex ist, ist der Bereich der zulässigen Werte eine konvexe Menge, die aufgerufen wird Polygon Entscheidungen. Die Seiten dieses Polygons liegen auf Geraden, deren Gleichungen aus dem ursprünglichen Zwangssystem durch Ersetzen von Ungleichheitszeichen durch Gleichheitszeichen erhalten werden.

Die Menge möglicher Lösungen für dieses spezielle Problem kann sein:

leerer Bereich;

konvexes Polygon, einschließlich entarteter Fälle – Liniensegment und einzelner Punkt;

konvexer, polygonaler, unbegrenzter Bereich, einschließlich der entarteten Fälle – Strahl und Linie.

Die praktische Umsetzung der Lösung des linearen Programmierproblems (1.6) – (1.7) auf der Grundlage seiner geometrischen Interpretation umfasst die folgenden Schritte:

1. Konstruieren Sie Geraden, deren Gleichungen durch Ersetzen der Ungleichheitszeichen in den Einschränkungen (1.7) durch Gleichheitszeichen erhalten werden.

2. Finden Sie die durch jede der Einschränkungen definierten Halbebenen.

Die entsprechende Halbebene kann gefunden werden, indem man einen „einfachen“ Punkt in die Koordinatenungleichung einsetzt – (0,0), (0,1) oder (1,0). Die Hauptsache ist, dass dieser Punkt nicht zur Grenze der Halbebene gehört. Wenn sich nach der Substitution herausstellt, dass die Ungleichung wahr ist, wird die Halbebene ausgewählt, die diesen Punkt enthält. Wenn die Ungleichung nicht wahr ist, wird eine alternative Halbebene ausgewählt.

3. Definieren Sie das Lösungspolygon als Schnittpunkt der gefundenen Halbebenen.

4. Konstruieren Sie den Gradienten der Zielfunktion, d. h. Vektor
, deren Koordinaten die Koeffizienten der Zielfunktion sind L.

Dieser Vektor bestimmt die Richtung des schnellsten Anstiegs der Zielfunktion.

5. Konstruieren Sie eine Reihe von Linien auf Zielfunktionsebene L, d.h. gerade Linien senkrecht zum Farbverlauf L. In diesem Fall sollte die Konstruktion von Niveaulinien in Richtung des Gradienten erfolgen, wenn das maximale Problem gelöst werden soll, und in der entgegengesetzten Richtung (in Richtung des „Antigradienten“), wenn das minimale Problem gelöst werden soll gelöst. Dadurch werden die Punkte markiert, an denen die Höhenlinien zuletzt die zulässige Menge berühren.

Wenn der zulässige Satz unbegrenzt ist, kann es sein, dass es keinen endgültigen Ansprechpartner gibt. Die Pegellinien gehen bis ins Unendliche, entsprechend dem Wert
oder
, und das Problem hat keine optimalen Pläne.

Bestimmen Sie die Koordinaten des markierten Punktes analytisch, indem Sie das entsprechende lineare Gleichungssystem lösen. Berechnen Sie dann den Wert der Zielfunktion an dieser Stelle. Somit werden der optimale Plan und der optimale Wert der Zielfunktion des Problems bestimmt.

Zum Abschluss unserer Betrachtung der geometrischen Interpretation des Problems (1.6) – (1.7) stellen wir fest, dass bei der Lösungsfindung die in Abb. 1.1 – 1.3. Reis. 1.1 charakterisiert den Fall, dass die Zielfunktion an einem einzelnen Punkt A, einem der Eckpunkte der zulässigen Menge, einen optimalen Wert annimmt. In Abb. 1.2 nimmt die Zielfunktion an jedem Punkt der Strecke AB ihren optimalen Wert an. In Abb. Abbildung 1.3 zeigt den Fall, dass der optimale Wert der Zielfunktion unerreichbar ist.

Reis. 1.1. Optimale Funktion L erreichbar am Punkt A

Reis. 1.2. Optimale Funktion L wird an jedem Punkt des Segments erreicht AB

Reis. 1.3. Optimale Funktion L unerreichbar