Как найти оптимальное решение производственного процесса. Какое решение можно считать оптимальным? Графоаналитический способ решения задач линейного программирования

Следует отметить, что методы решения задач линейного программирования относятся не к экономике, а к математике и вычислительной технике. При этом экономисту нужно обеспечить максимально комфортные условия диалога с соответствующим программным обеспечением. В свою очередь такие условия могут обеспечивать только динамично развивающиеся и интерактивные среды разработки, имеющие в своём арсенале набор необходимых для решения таких задач библиотек. Одной из каких сред разработки программного обеспечения безусловно является Python.

Постановка задачи

В публикациях рассматривались решения прямых задач оптимизации методом линейного программирования и был предложен обоснованный выбор решателя scipy. optimize.

Однако известно , что каждой задаче линейного программирования соответствует так называемая выделенная(двойственная)задача. В ней по сравнению с прямой задачей строки переходят в столбцы, неравенства меняют знак, вместо максимума ищется минимум (или наоборот, вместо минимума - максимум). Задача, двойственная к двойственной - эта сама исходная задача.

Решение двойственной задачи очень важно для анализа использования ресурсов. В данной публикации будет доказано, что оптимальные значения целевых функций в исходной и двойственной задачах совпадают (т.е. максимум в исходной задаче совпадает с минимумом в двойственной).

Оптимальные значения стоимости материала и труда будут оцениваться по их вкладу в целевую функцию. В результате будут получены «объективно обусловленные оценки» сырья и рабочей силы, которые не совпадают с рыночными ценами.

Решение прямой задачи о оптимальной производственной программе

Учитывая высокий уровень математической подготовки подавляющего большинства пользователей данного ресурса не стану приводить балансовые уравнения с верхними и нижними ограничениями и введением для перехода к равенствам дополнительных переменных. Поэтому сразу приведу обозначения используемых в решении переменных:
N – количество видов производимых изделий;
m– количество видов используемого сырья;
b_ub - вектор имеющихся ресурсов размерности m;
A_ub – матрица размерности m×N, каждый элемент которой является расходом ресурса вида i на производство единицы изделия вида j;
с - вектор прибыли от производства единицы изделия каждого вида;
x – искомые объёмы производимых изделий каждого вида (оптимальный план производства) обеспечивающие максимальную прибыль.

Функция цели
maxF(x)=c×x

Ограничения
A×x≤b

Численные значения переменных:
N=5; m=4; b_ub = ; A_ub = [, , ,]; c = .

Задачи
1.Найти x для обеспечения максимальной прибыли
2. Найти использованные ресурсы при выполнении п.1
3. Найти остатки ресурсов (если они есть) при выполнении п.1

Для определения максимума (по умолчанию определяется минимум коэффициенты целевой функции нужно записать с отрицательным знаком c = [-25, -35,-25,-40,-30] и проигнорировать знак минус перед прибылью.

Используемые при выводе результатов обозначения:
x – массив значений переменных, доставляющих минимум (максимум) целевой функции;
slack – значения дополнительных переменных. Каждая переменная соответствует ограничению-неравенству. Нулевое значение переменной означает, что соответствующее ограничение активно;
success – True, если функции удалось найти оптимальное решение;
status – статус решения:
0 – поиск оптимального решения завершился успешно;
1 – достигнут лимит на число итераций;
2 – задача не имеет решений;
3 – целевая функция не ограничена.
nit – количество произведенных итераций.

Листинг решения прямой задачи оптимизации

#!/usr/bin/python # -*- coding: utf-8 -*- import scipy from scipy.optimize import linprog # загрузка библиотеки ЛП c = [-25, -35,-25,-40,-30] # список коэффициентов функции цели b_ub = # список объёмов ресурсов A_ub = [, # матрица удельных значений ресурсов , , ] d=linprog(c, A_ub, b_ub) # поиск решения for key,val in d.items(): print(key,val) # вывод решения if key=="x": q=#использованные ресурсы print("A_ub*x",q) q1= scipy.array(b_ub)-scipy.array(q) #остатки ресурсов print("b_ub-A_ub*x", q1)

Результаты решения задачи
nit 3
status 0

success True
x [ 0. 0. 18.18181818 22.72727273 150. ]
A_ub*x
b_ub-A_ub*x [ 0. 0. 0. 90.90909091]
fun -5863.63636364
slack [ 0. 0. 0. 90.90909091]

Выводы

1. Найден оптимальный план по видам продукции
2. Найдено фактическое использование ресурсов
3. Найден остаток не использованного четвёртого вида ресурса [ 0. 0 0.0 0.0 90.909]
4. Нет необходимости в вычислениях по п.3, так как тот же результат выводить в переменной slack

Решение двойственной задачи о оптимальной производственной программе

Четвёртый вид ресурса в прямой задаче использована не полностью. Тогда ценность этого ресурса для предприятия оказывается более низкой по сравнению с ресурсами, ограничивающими выпуск продукции, и предприятие готово заплатить более высокую цену за приобретение ресурсов, позволяющих увеличить прибыль.

Введём новое назначение искомой переменной x как некоторой «теневой» цены, определяющей ценность данного ресурса в отношении прибыли от реализации выпускаемой продукции.

C – вектор имеющихся ресурсов;
b_ub – вектор прибыли от производства единицы изделия каждого вида;
A_ub_T– транспонированная матрица A_ub.

Функция цели
minF(x)=c×x

Ограничения
A_ub_T ×x≥ b_ub

Численные значения и соотношения для переменных:
с = ; A_ub_T transpose(A_ub); b_ub = .

Задача:
Найти x показывающий ценность для производителя каждого вида ресурсов.

Особенности решения с библиотекой scipy. optimize
Для замены ограничений сверху на ограничения с низу необходимо умножить на минус единицу обе части ограничения – A_ub_T ×x≥ b_ub… Для этого исходные данные записать в виде: b_ub = [-25, -35,-25,-40,-30]; A_ub_T =- scipy.transpose(A_ub).

Листинг решения двойственной задачи оптимизации

#!/usr/bin/python # -*- coding: utf-8 -*- import scipy from scipy.optimize import linprog A_ub = [, , , ] c= b_ub = [-25, -35,-25,-40,-30] A_ub_T =-scipy.transpose(A_ub) d=linprog(c, A_ub_T, b_ub) for key,val in d.items(): print(key,val)

Результаты решения задачи
nit 7
message Optimization terminated successfully.
fun 5863.63636364
x [ 2.27272727 1.81818182 6.36363636 0. ]
slack [ 5.45454545 2.27272727 0. 0. 0. ]
status 0
success True

Выводы

Третий вид ресурсов имеет наибольшую ценность для производителя поэтому данный вид ресурсов должен быть закуплен в первую очередь, затем первый и второй вид. Четвёртый вид ресурса имеет для производителя нулевую ценность и закупается последним.

Результаты сравнения прямой и двойственной задачи

1. Двойственная задача расширяет возможности планирования выпуска продукции, но средствами scipy. optimize решается за вдвое большее чем прямая количество итераций.
2. Переменная slack выводит информацию об активности ограничений в виде неравенств, что может быть использовано, например, для анализа остатков сырья.
3. Прямая задача является задачей максимизации, а двойственная - задачей минимизации, и наоборот.
4. Коэффициенты функции цели в прямой задаче являются ограничениями в двойственной задаче.
5. Ограничения в прямой задаче становятся коэффициентами функции цели в двойственной.
6. Знаки неравенств в ограничениях меняются на противоположные.
7. Матрица системы равенств транспонируется.

Ссылки Оптимизация линейных моделей в MS Excel производится симплекс-методом - целенаправленным перебором опорных решений задачи линейного программирования. Алгоритм симплекс-метода сводится к построению выпуклого многогранника в многомерном пространстве, а затем к перебору его вершин с целью поиска экстремального значения целевой функции .

Эффективные средства линейного программирования лежат в основе и целочисленного и нелинейного программирования для решения более сложных задач оптимизации. Эти методы, однако, требуют более длительного времени для вычислений.

В последующих лекциях будут подробно разобраны примеры решения типичных задач оптимизации и принятия управленческих решений с помощью надстройки MS Excel " Поиск решения". Задачи, которые лучше всего решаются данным средством, имеют три основных свойства:

• имеется единственная цель, функционально связанная с другими параметрами системы, которую нужно оптимизировать (найти ее максимум, минимум или определенное числовое значение);
• имеются ограничения, выражающиеся, как правило, в виде неравенств (например, объем используемого сырья не может превышать запасов сырья на складе, или время работы станка за сутки не должно быть больше 24 часов минус время на обслуживание);
• имеется набор входных значений-переменных, влияющих на оптимизируемые величины и на ограничения.

Параметры задач ограничиваются такими предельными показателями:

• количество неизвестных – 200;
• количество формульных ограничений на неизвестные – 100;
• количество предельных условий на неизвестные – 400.

Алгоритм поиска оптимальных решений включает в себя несколько этапов:

• подготовительные работы;
• отладка решения;
• анализ решения .

Последовательность необходимых подготовительных работ , выполняемых при решении задач экономико-математического моделирования с помощью MS Excel , приведена на блок-схеме рисунка 1.6 .

Рис. 1.6.

Из приведенных пяти пунктов плана подготовительных работ только пятый пункт является формализуемым. Остальные работы требуют творчества - и разными людьми они могут быть выполнены по -разному. Кратко поясним сущность формулировок пунктов плана.

При постановке задачи известны целевые коэффициенты и нормированные коэффициенты . В предыдущем примере коэффициентами, формирующими целевую функцию, служили значения нормированной прибыли на одну полку типа () и одну полку типа (). Нормированными коэффициентами служили нормы расхода материала и машинного времени на одну полку каждого типа. Матрица имела следующий вид:

Кроме того, всегда известны значения ресурсов . В предыдущем примере это был недельный запас досок и возможности использовать машинное время: , . Часто в задачах значения переменных требуется ограничить. Поэтому нужно определить нижний и верхний пределы области их изменений.

Таким образом, в диалоговом окне оптимизационной программы " Поиск решения" мы должны задать следующий целевой алгоритм :

Целевая функция равна произведению вектора искомых значений переменных на вектор целевых коэффициентов

Нормированных коэффициентов на вектор искомых значений переменных не должен превышать значения заданного вектора ресурсов

Значения переменной должны находиться в заданных пределах число исходных элементов системы

Число исходных элементов системы

Число заданных видов ресурсов

Отладка решения необходима в случае, когда программа выдает сообщение об отрицательных результатах (рисунок 1.7):

Рис. 1.7.

• если не получено допустимое решение, то выполнить корректировку модели исходных данных;
• если не получено оптимальное решение , то ввести дополнительные ограничения.

Программа выдает оптимальное решение только для модели реальной проблемы, а не решение самой проблемы. При построении модели были сделаны различные упрощающие допущения реальной ситуации. Это позволило формализовать процесс, приближенно отобразив реальные количественные зависимости между параметрами системы и целью. А если реальные параметры будут отличаться от тех, которые заложены в модели, то как изменится решение? Чтобы узнать это, перед принятием управленческого решения проводят анализ решения модели.

Анализ оптимального решения , встроенный в программу, представляет собой заключительный этап математического моделирования экономических процессов. Он позволяет осуществить более глубокую проверку соответствия модели процессу, а также надежности оптимального решения. Он основывается на данных оптимального решения и отчетов, которые выдаются в "Поиске решения". Но он не исключает и не заменяет традиционного анализа плана с экономических позиций перед принятием управленческого решения.

Экономический анализ ставит перед собой следующие цели :

• определение возможных последствий в системе в целом и ее элементах при изменении параметра модели;
• оценка устойчивости оптимального плана к изменению отдельных параметров задачи: если он не устойчив к изменению большинства параметров, снижается гарантия его выполнения и достижения рассчитанного оптимума;
• проведение вариантных расчетов и получение новых вариантов плана без повторного решения задачи от исходного базиса с помощью корректировки.

Возможные методы анализа представлены в схеме на рисунке 1.8 .

После получения оптимального решения проводится его анализ по полученным отчетам. Анализ устойчивости - изучение влияния изменений отдельно взятых параметров модели на показатели оптимального решения. Анализ пределов - анализ допустимых изменений в оптимальном плане, при котором план остается оптимальным.

Учитывая ответственность принятия экономического управленческого решения , руководитель должен убедиться, что полученный оптимальный план является единственно верным. Для этого надо на основе модели получить ответы на следующие вопросы:

• "что будет, если…"
• "что надо, чтобы…"

Анализ с целью ответа на первый вопрос называется вариантным анализом ; анализ с целью ответа на второй вопрос называется решениями по заказу.

Вариантный анализ бывает следующих видов:

• Параметрический - анализ, который заключается в решении задачи при различных значениях некоторого параметра.
• Структурный анализ - когда решение задачи оптимизации ищется при различной структуре ограничений.
• Многокритериальный анализ - это решение задачи по разным целевым функциям.
• Анализ при условных исходных данных - когда исходные данные, используемые при решении задачи, зависят от соблюдения дополнительных условий.

После проведения анализа следует представить результаты в графической форме и составить отчет с рекомендациями о принятии решения с учетом конкретной экономической ситуации.

Универсальный метод решения задач ЛП называется симплекс-методом. Применение этого метода и его наиболее часто встречающейся модификации - двухфазного симплекс-метода.

При графическом методе решения задач ЛП мы фактически из множества вершин, принадлежащих границе множества решений системы неравенств, выбрали такую вершину, в которой значение целевой функции достигало максимума (минимума). В случае двух переменных этот метод совершенно нагляден и позволяет быстро находить решение задачи.

Если в задаче три и более переменных, а в реальных экономических задачах как раз такая ситуация, трудно представить наглядно область решений системы ограничений. Такие задачи решаются с помощью симплекс-метода или методом последовательных улучшений. Идея метода проста и заключается в следующем.

По определенному правилу находится первоначальный опорный план (некоторая вершина области ограничений). Проверяется, является ли план оптимальным. Если да, то задача решена. Если нет, то переходим к другому улучшенному плану - к другой вершине. значение целевой функции на этом плане (в этой вершине) заведомо лучше, чем в предыдущей. Алгоритм перехода осуществляется с помощью некоторого вычислительного шага, который удобно записывать в виде таблиц, называемых симплекс-таблицами . Так как вершин конечное число, то за конечное число шагов мы приходим к оптимальному решению.

Рассмотрим симплексный метод на конкретном примере задачи о составлении плана.

Еще раз заметим, что симплекс-метод применим для решения канонических задач ЛП, приведенных к специальному виду, т. е. имеющих базис, положительные правые части и целевую функцию, выраженную через небазисные переменные. Если задача не приведена к специальному виду, то нужны дополнительные шаги, о которых мы поговорим позже.

Рассмотрим задачу о плане производства, предварительно построив модель и приведя ее к специальному виду.

Задача.

Для изготовления изделий А и В склад может отпустить сырья не более 80 единиц. Причем на изготовление изделия А расходуется две единицы, а изделия В - одна единица сырья. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если изделий А требуется изготовить не более 50 шт., а изделий В - не более 40 шт. Причем, прибыль от реализации одного изделия А - 5 руб., а от В - 3 руб.

Построим математическую модель, обозначив за х 1 количество изделий А в плане, за х 2 - количество изделий В . тогда система ограничений будет выглядеть следующим образом:

x 1 ≤50
x 2 ≤40
2x 1 +x 2 ≤80
x 1 ≥0, x 2 ≥0
5x 1 +3x 2 →max

Приведем задачу к каноническому виду , введя дополнительные переменные:

x 1 +x 3 =50
x 2 +x 4 =40
2x 1 +x 2 +x 5 =80
x 1 ≥0, x 2 ≥0
5x 1 +3x 2 →max
-F = -5x 1 - 3x 2 → min.

Эта задача имеет специальный вид (с базисом, правые части неотрицательны). Ее можно решить симплекс-методом.

I этап. Запись задачи в симплекс-таблицу. Между системой ограничений задачи (3.10) и симплекс-таблицей взаимно-однозначное соответствие. Строчек в таблице столько, сколько равенств в системе ограничений, а столбцов - столько, сколько свободных переменных. Базисные переменные заполняют первый столбец, свободные - верхнюю строку таблицы. Нижняя строка называется индексной, в ней записываются коэффициенты при переменных в целевой функции. В правом нижнем углу первоначально записывается 0, если в функции нет свободного члена; если есть, то записываем его с противоположным знаком. На этом месте (в правом нижнем углу) будет значение целевой функции, которое при переходе от одной таблицы к другой должно увеличиваться по модулю. Итак, нашей системе ограничений соответствует таблица 3.4, и можно переходить ко II этапу решения.

Таблица 3.4

базисные			свободные

II этап . Проверка опорного плана на оптимальность.

Данной таблице 3.4 соответствует следующий опорный план:

(х 1 , х 2 , х 3 , х 4 , х 5) = (0, 0, 50, 40, 80).

Свободные переменные х 1 , х 2 равны 0; х 1 = 0, х 2 = 0. А базисные переменные х 3 , х 4 , х 5 принимают значения х 3 = 50, х 4 = 40, х 5 = 80 - из столбца свободных членов. Значение целевой функции:

-F = - 5х 1 - 3х 2 = -5 · 0 - 3 · 0 = 0.

Наша задача - проверить, является ли данный опорный план оптимальным. для этого необходимо просмотреть индексную строку - строку целевой функции F .

Возможны различные ситуации.

1. В индексной F -строке нет отрицательных элементов. Значит, план оптимален, можно выписать решение задачи. Целевая функция достигла своего оптимального значения, равного числу, стоящему в правом нижнем углу, взятому с противоположным знаком. Переходим к IV этапу.

2. В индексной строке есть хотя бы один отрицательный элемент, в столбце которого нет положительных. Тогда делаем вывод о том, что целевая функция F →∞ неограниченно убывает.

3. В индексной строке есть отрицательный элемент, в столбце которого есть хотя бы один положительный. Тогда переходим к следующему III этапу. пересчитываем таблицу, улучшая опорный план.

III этап . Улучшение опорного плана.

Из отрицательных элементов индексной F -строки выберем наибольший по модулю, назовем соответствующий ему столбец разрешающим и пометим "".

Чтобы выбрать разрешающую строку, необходимо вычислить отношения элементов столбца свободных членов только к положительным элементам разрешающего столбца. Выбрать из полученных отношений минимальное. Соответствующий элемент, на котором достигается минимум, называется разрешающим. Будем выделять его квадратом.

В нашем примере, элемент 2 - разрешающий. Строка, соответствующая этому элементу, тоже называется разрешающей (табл. 3.5).

Таблица 3.5

Выбрав разрешающий элемент, делаем перечет таблицы по правилам:

1. В новой таблице таких же размеров, что и ранее, переменные разрешающей строки и столбца меняются местами, что соответствует переходу к новому базису. В нашем примере: х 1 входит в базис, вместо х 5 , которая выходит из базиса и теперь свободная (табл. 3.6).

Таблица 3.6

2. На месте разрешающего элемента 2 записываем обратное ему число ½.

3. Элементы разрешающей строки делим на разрешающий элемент.

4. Элементы разрешающего столбца делим на разрешающий элемент и записываем с противоположным знаком.

5. Чтобы заполнить оставшиеся элементы таблицы 3.6, осуществляем пересчет по правилу прямоугольника. Пусть мы хотим посчитать элемент, стоящий на месте 50.

Соединяем этот элемент мысленно с разрешающим, находим произведение, вычитаем произведение элементов, находящихся на другой диагонали получившегося прямоугольника. Разность делим на разрешающий элемент.

Итак, . Записываем 10 на место, где было 50. Аналогично:
, , , .

Таблица 3.7

Имеем новую таблицу 3.7, базисными переменными теперь являются переменные {x 3 ,x 4 ,x 1 }. Значение целевой функции стало равно -200, т.е. уменьшилось. Чтобы проверить данное базисное решение на оптимальность надо перейти опять ко II этапу. Процесс, очевидно, конечен, критерием остановки являются пункт 1 и 2 II этапа.

Доведем решение задачи до конца. Для этого проверим индексную строку и, увидев в ней отрицательный элемент -½, назовем соответствующий ему столбец разрешающим и, согласно III этапу, пересчитаем таблицу. Составив отношения и выбрав среди них минимальное = 40, определили разрешающий элемент 1. теперь пересчет осуществляем согласно правилам 2-5.

Таблица 3.8

После пересчета таблицы убеждаемся, что в индексной строке нет отрицательных элементов, следовательно, задача решена, базисный план оптимален.

IV этап . Выписывание оптимального решения.

Если симплекс-метод остановился согласно пункту 1 II этапа, то решение задачи выписывается следующим образом. Базисные переменные принимают значения столбца свободных членов соответственно. В нашем примере х 3 = 30, х 2 = 40, х 1 = 20. Свободные переменные равны 0, х 5 = 0, х 4 = 0. Целевая функция принимает значение последнего элемента столбца свободных членов с противоположным знаком: -F = -220 → F = 220, в нашем примере функция исследовалась на min, и первоначально F → max, поэтому фактически знак поменялся дважды. Итак, х * = (20, 40, 30, 0, 0), F * = 220. Ответ к задаче:

Необходимо в план выпуска включить 20 изделий типа А , 40 изделий типа В, при этом прибыль будет максимальной и будет равна 220 руб.

В конце этого параграфа приведем блок-схему алгоритма симплекс-метода, которая в точности повторяет этапы, но, возможно, для некоторых читателей будет более удобна в пользовании, т. к. стрелочки указывают четкую направленность действий.

Ссылки над прямоугольниками в блок-схеме показывают, к какому этапу или подпункту относится соответствующая группа преобразований. правило нахождения первоначального опорного плана будет сформулировано в пункте 3.7.

Пример . Решить следующую задачу ЛП в канонической форме симплекс-методом.
f(x)=x 1 +9x 2 +5x 3 +3x 4 +4x 5 +14x 6 → min
x 1 +x 4 =20
x 2 +x 5 =50
x 3 +x 6 =30
x 4 +x 5 +x 6 =60
x i ≥ 0, i = 1,…,6
Говорят, что задача ЛП имеет каноническую форму, если все ограничения (кроме условий неотрицательности переменных) имеют вид равенств, а все свободные члены неотрицательны. Так что мы имеем задачу в канонической форме.
Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).
Таким образом, идея симплекс-метода основывается на трех свойствах задачи ЛП.
Решение. Чтобы найти начальное допустимое базисное решение, т.е. чтобы определить базисные переменные, систему (5.6) нужно привести к "диагональному" виду. Применяя метод Гаусса (метод последовательного исключения неизвестных), получаем из (5.6):
x 2 +x 1 +x 3 =40
x 4 +x 1 =20
x 5 -x 1 -x 3 =10
x 6 +x 3 =30
Следовательно, базисными являются переменные x 2 , x 4 , x 5 , x 6 , им придаем значения, равные свободным членам соответствующих строк: x 2 =40, x 4 =20, x 5 =10, x 6 =30, . Переменные x 1 и x 3 являются небазисными: x 1 =0, x 3 =0 .
Построим начальное допустимое базисное решение
x 0 = (0,40,0,20,10,30) (5.9)
Для проверки на оптимальность найденного решения x 0 нужно из целевой функции исключить базисные переменные (с помощью системы (5.8)) и построить специальную симплекс таблицу.
После исключения переменных целевую функцию удобно записать в виде:
f(x) = -7x 1 – 14x 3 +880 (5.10)
Теперь при помощи (5.8) –(5.10) составляем начальную симплекс-таблицу:

В нулевую строчку записаны коэффициенты с обратным знаком соответствующих переменных при целевой функции. Критерий оптимальности (для задачи на поиск минимума): допустимое базисное решение(x 0 ) оптимально, если в нулевой строчке нет ни одного строго положительного числа (не считая значения целевой функции (880)). Это правило распространяется и на следующие итерации (таблицы). Элементы нулевой строки будем называть оценками столбцов.
Так что начальное допустимое базисное решение (5.9) неоптимально: 7>0, 14>0 .
В нулевом столбике записаны значения базисных переменных. Они обязательно должны быть неотрицательными (см. уравнение (5.7)). От первой по четвертую строки написаны коэффициенты переменных из системы (5.8).
Так как x 0 неоптимально, то надо перейти к другой вершине многогранника допустимых решений (построить новое д.б.р.). Для этого нужно найти ведущий элемент и провести определенное преобразование (симплексное преобразование).
Сначала находим ведущий элемент таблицы, который стоит в пересечении ведущего столбика (столбец с наибольшей положительной оценкой) и ведущей строки (строки, соответствующей минимальному соотношению элементов нулевого столбика к соответствующим элементам (строго положительным) ведущего столбика).
В таблице 1 ведущий столбик - третий столбик, и ведущая строка - четвертая строка (min{40/1,30/1}=30/1) обозначены стрелками, а ведущий элемент - кружочком. Ведущий элемент показывает, что базисную переменную x 6 нужно заменить на небазисную x 3 . Тогда новыми базисными переменными будут x 2 , x 3 , x 4 , x 5 , , а небазисными -x 1 , x 6 , . Это и означает переход к новой вершине многогранника допустимых решений. Чтобы найти значения координат нового допустимого базисного решения x 00 нужно строить новую симплекс-таблицу и провести в ней элементарные преобразования:
а) все элементы ведущей строки поделить на ведущий элемент, превратив этим самым ведущий элемент в 1 (для простоты выкладок);
б) с помощью ведущего элемента (равного 1) все элементы ведущего столбика превратить в нули (аналогично методу исключения неизвестных);
В результате в нулевом столбце получены значения новых базисных переменных x 2 , x 3 , x 4 , x 5 , (см. таблицу 2) - базисные компоненты новой вершины x 00 (небазисные компоненты x 1 =0, x 6 =0, ).

Как показывает таблица 2, новое базисное решение x 00 =(0,10,30,20,40,0) неоптимально (в нулевой строке есть неотрицательная оценка 7). Поэтому с ведущим элементом 1 (см. таблицу 2) строим новую симплекс-таблицу, т.е. строим новое допустимое базисное решение

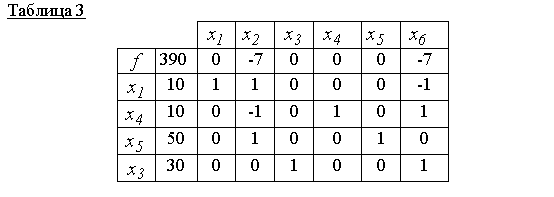
Таблице 3 соответствует допустимое базисное решение x 000 =(10,0,30,10,50,0) и оно оптимально, т.к. в нулевой строчке нет положительных оценок. Поэтому f(x 000)=390 есть минимальное значение целевой функции.
Ответ: x 000 =(10, 0, 30, 10, 50, 0) - точка минимума, f(x 000)=390 .

Условно стандартная задача линейного программирования

Необходимо выполнить в указанном порядке следующие задания.

1. Найти оптимальный план прямой задачи:
   а) графическим методом ;
   б) симплекс-методом (для построения исходного опорного плана рекомендуется использовать метод искусственного базиса).
2. Построить двойственную задачу .
3. Найти оптимальный план двойственной задачи из графического решения прямой, используя условия дополняющей нежесткости.
4. Найти оптимальный план двойственной задачи по первой теореме двойственности , используя окончательную симплекс-таблицу, полученную при решении прямой задачи (см. п. 1б). Проверить утверждение «значения целевых функций пары двойственных задач на своих оптимальных решениях совпадают».
5. Двойственную задачу решить симплекс-методом, затем, используя окончательную симплекс-таблицу двойственной задачи найти оптимальный план прямой задачи по первой теореме двойственности. Сравнить результат с результатом, который был получен графическим методом (см. п. 1а).
6. Найти оптимальное целочисленное решение:
   а) графическим методом ;
   б) Методом Гомори .
   Сравнить значения функций целочисленного и нецелочисленного решений

Вопросы для самоконтроля

1. Как строится симплекс-таблица?
2. Как отражается смена базиса в таблице?
3. Сформулируйте критерий остановки симплекс-метода.
4. Как организовать пересчет таблицы?
5. С какой строки удобно начинать пересчет таблицы?

Если в только что рассмотренной задаче первое же полученное базисное решение оказалось допустимым, то в других случаях его можно найти не сразу, а через некоторое число шагов.

При этом надо помнить, что на первом этапе симплексного метода, т. е. при нахождении какого-либо допустимого решения, линейная форма в расчет не берется, а все преобразования относятся только к системе ограничений.

Пусть задача линейного программирования задана в общем виде, т.е. системой m линейных уравнений с n переменными (m

Следовательно, этому способу разбиения переменных на основные и неосновные соответствует базисное решение …; 0; 0;…;0.

Рассмотрим общий случай, когда это решение является недопустимым. От полученного базисного решения следует сначала перейти к какому-нибудь допустимому базисному решению, причем не обязательно, чтобы этот переход осуществлялся сразу, в один шаг.

Если система ограничений не противоречива, то через конечное число шагов будет осуществлен переход к допустимому базисному решению.

По предположению, исходное базисное решение является недопустимым. Следовательно, среди свободных членов системы ограничений имеется хотя бы один отрицательный (число отрицательных свободных членов этой системы совпадает с числом отрицательных компонент исходного базисного решения). Пусть им является свободный член k i i-ro уравнения, т. е. основная переменная x i в соответствующем базисном решении отрицательна.

Для перехода к новому базисному решению необходимо решить два вопроса:

1) установить, какая неосновная переменная должна быть переведена в число основных;

2) выбрать переменную, которую из основных следует пере­вести в неосновные на место выбывшей в основные переменной.

При переводе неосновной переменной в основные она не убывает, а, как правило, возрастает: вместо нуля в исходном базисном решении она примет положительное значение в новом базисном решении (исключение имеет место только при вырождении). Поэтому для решения вопроса о том, какие неосновные переменные можно перевести в основные, нужно уметь находить неосновные переменные, при увеличении которых возрастает основная переменная, от­рицательная в исходном базисном решении. Вернемся к i-му уравнению системы, в котором свободный член k i отрицателен. Оно показывает, что переменная x i возрастает при возрастании тех неосновных переменных, коэффициенты которых в этом уравнении положительны. Отсюда следует, что в основные можно переводить те неосновные переменные, которые в уравнении системы с отрицательным свободным членом имеют положительные коэффициенты.

Здесь могут представиться три случая.

1. В i-м уравнении системы нет неосновных переменных с положительными коэффициентами, т. е. все коэффициенты b i , j отрицательны (как и свободный член k i). В этом случае данная система ограничений несовместна – она не имеет ни одного допустимого решения. Действительно, вследствие неотрицательности всех переменных, в том числе x m + l ,...,x n , i -го уравнения, в котором свободный член k i и все коэффициенты b i , m + l ,...,b i , n отрицательны, следует, что переменная x i - не может принимать неотрицательных значений. Но если нет ни одного допустимого решения системы ограничений, то нет и оптимального.

2. В i-м уравнении имеется одна переменная х т+ j ,коэффициентпри которой положителен. В этом случае именно эта переменная переводится в основные.

3. В i-м уравнении имеется несколько переменных с положительными коэффициентами. В этом случае в основные можно перевести любую из них.

Далее необходимо установить, какая основная переменная должна быть переведена в число неосновных. Для этого следует воспользоваться правилом: находят отношения свободных членов к коэффициентам при переменной, переводимой в основные, из всех уравнений, где знаки свободных членов и указанных коэффициентов противоположны, а затем рассматривают абсолютную величину этих отношений и из них выбирают наименьшую (если в некоторых уравнениях знаки свободных членов и коэффициентов совпадают или в каких-то уравнениях переменная, переводимая в основные, отсутствует, то отношение считают равным ∞).

Уравнение, из которого получено наименьшее отношение, выделяют. Выделенное уравнение показывает, какая из основных переменных должна быть переведена в неосновные. Выразив новые основные переменные через неосновные, переходят к следующему базисному решению.

В результате получается аналогичная системе система уравнений, в которой число отрицательных свободных кленов либо совпадает с их числом в системе, либо на единицу меньше. Это зависит от того, положителен или отрицателен свободный член в выделенном уравнении.

Если в выделенном уравнении свободный член отрицателен, то в новом базисном решении число отрицательных компонент окажется на единицу меньше, чем в исходном. Если же в выделенном уравнении свободный член положителен (или равен нулю), то в новом базисном решении число отрицательных компонент останется таким же, как и в исходном.

Итак, получается новое, улучшенное базисное решение, которое ближе к области допустимых решений системы ограничений. Если оно окажется недопустимым, то к нему следует применить ту же схему еще раз. В результате через конечное число шагов получится допустимое базисное решение.

Продолжения примера 4.1. Нужно найти такое допустимое базисное решение этой системы ограничений, которое бы максимизировало линейную форму .

Так как система ограничений есть система четырех независимых уравнений с шестью переменными, то число основных переменных должно равняться четырем, а число неосновных - двум.

Для решения задачи симплексным методом, прежде всего, нужно найти любое базисное решение. В данном случае это легко сделать. Для этого достаочно взять в качестве основных добавочные переменные х 3 , х 4 , х 5 , х 6 . Так как коэффициенты при этих переменных образуют единичную матрицу, то отпадает необходимость вычислять определитель. Считая неосновные переменные х 1 , x 2 равными нулю, получим базисное решение (0; 0; 120; 160; 120; 80), которое к тому же оказалось допустимым. Поэтому здесь отпадает надобность в применении первого этапа симплексного метода.

Переходим сразу ко второму этапу, т. е. к поискам оптимального решения.

1 шаг. Основные переменные: х 3 , х 4 , х 5 , х 6 ; неосновные переменные: х 1 , x 2 . В системе основные переменные выразим через неосновные. Для того чтобы судить, оставить ли неосновные переменные в числе неосновных или их выгоднее с точки зрения приближения к оптимальному решению перевести в основные, следует выразить через них и линейную форму (в данном случае она уже выражена через переменные х 1 , x 2) Тогда получим:

При х 1 = х 2 = 0 имеем х 3 = 120, х 4 = 160, х 5 = 120, х 6 = 80, что дает базисное решение (0; 0; 120; 160; 120; 80), которое мы приняли за исходное. При этом базисном решении значение линейной формы =0.

Когда мы полагали х 1 = х 2 = 0 (производство ничего не выпускает), была поставлена цель - найти первое, безразлично какое, базисное решение. Эта цель достигнута. Теперь от этого первоначального решения нужно перейти к другому, при котором значение линейной формы увеличится. Из рассмотрения линейной формы видно, что ее значение возрастает при увеличении значений переменных х 1 и х 2 . Иными словами, эти переменные невыгодно считать неосновными, т. е. равными нулю, их нужно перевести в число основных. Это и оз­начает переход к новому базисному решению. При симплексном методе на каждом шаге решения предполагается перевод в число основных только одной из свободных переменных. Переведем в число основных переменную х 2 , так как она входит в выражение линейной формы с большим коэффициентом.

Как только одна из свободных переменных переходит в число основных, одна из основных должна быть переведена на ее место в число неосновных. Какую же из четырех основных переменных нужно вывести? Ответить на этот вопрос помогут следующие рассуждения.

Значение х 2 необходимо сделать как можно большим, так как это соответствует конечной пели - максимизации F . Однако оказывается, что увеличение х 2 может продолжаться только до известных границ, а именно до тех пор, пока не нарушится требование неотрицательности переменных. Так, из первого уравнения системы следует, что переменная х 2 не должна превышать числа 120/4, т. е. х 2 ≤30, поскольку только при этих значениях х 2 переменная х 3 остается положительной (если х 2 = 30, то х 3 = 0; если же х 2 >30, то х 3 < 0). Из третьего уравнения системы следует, что х 2 ≤ 120/2, т. е. х 2 ≤ 60, из четвертого - что х 2 ≤ 80/2, т. е. х 2 ≤ 40 (во второе уравнение переменная х 2 не входит). Всем этим условиям удовлетворяет х 2 ≤ 30.

Иными словами, для ответа на вопрос, какую переменную нужно пере­вести в число неосновных, нужно принять х 2 = min {120/4; 120/2; 80/2} = min {30; 60; 40} = 30. Тогда х 3 = 0 и х 3 переходит в число неосновных переменных, а х 4 и х 5 останутся положительными,

2 шаг. Основные переменные: х 2 , х 4 , х 5 , х 6 неосновные переменные: х 1 и х 3 . Выразим основные переменные и линейную форму через неосновные. В системе берем то уравнение, из которого получено минимальное значение отношения свободного члена к коэффициенту при х 2 . В данном случае это первое уравнение. Выразив из этого уравнения х 2 , имеем, х 2 = 30 - 0.25 · х 3 . Подставим это выражение х 2 во все остальные уравнения системы (4.4) и в линейную форму F и, приведя подобные члены, получим

При х 1 = х 3 = 0 имеем F = 90. Это уже лучше, чем на 1 шаге, но не искомый максимум. Дальнейшее увеличение функции F возможно за счет введения переменной х 1 в число основных; так как эта переменная входит в выражение F с положительным коэффициентом, поэтому ее увеличение приводит к увеличению линейной формы и ее невыгодно считать неосновной, т.е. равной нулю.

Для ответа на вопрос, какую переменную вывести из основных в неосновные, примем х 1 = min {160/4; 60/2; 20/1} = 20. Тогда х 6 = 0 и х 6 переходит в число неосновных переменных, а х 4 и х 5 , остаются при этом положительными.

Первое уравнение не используется при нахождении указанного минимума, так как х ] не входит в это уравнение.

3 шаг. Основные переменные: х 1 ,х 2 , х 4 , х 5 ; неосновные переменные: х 3 , х 6 . Выразим основные переменные и линейную форму через неосновные. Из последнего уравнения системы (4.5) (оно выделено) имеем х 1 = 20 + 0.5 · х 3 - х 6 . Подставляя это выражение в остальные уравнения и в линейную форму, получим

Из выражения линейной формы следует, что ее максимальное значение еще не получено, так как возможно увеличение F за счет введения в основные переменной х 3 (она имеет положительный коэффициент). Полагаем х 3 = min {∞; 30/0,25; 80/2; 20/0,5} =40.

Здесь мы впервые встречаемся с двумя положениями, которые требуют дополнительных разъяснений.

Во-первых, хотя переменная х 3 и входит в выражение для х 1 (первое уравнение системы (4.6), но имеет положительный коэффициент и при любом возрастании х 3 переменная х 1 не может стать отрицательной. Иными словами, в первом уравнении никаких ограничений на возрастание переменной х 3 не накладывается, поэтому мы условно пишем ∞. Условимся в дальнейшем пользоваться этим же обозначением, если переменная, вновь вводимая в число основных, не входит в какое-либо уравнение системы ограничении.

Во-вторых, мы получим два одинаковых минимальных значения, равные 40. Если х 3 = 40, то х 4 = 0 и х 5 = 0, т. е. напрашивается вывод, что вместо одной переменной нужно перевести в число неосновных сразу две: х 4 и х 5 . Но число основных переменных не должно быть меньше четырех. Для этого поступают следующим образом. Одну из переменных (х 4 или х 5 .) оставляют в числе основных, но при этом ее значение считают равным нулю, т. е. полученное на следующем шаге базисное решение оказывается вырожденным. Оставим, например, х 4 в числе основных переменных, а х 5 переведем в число неосновных.

4 шаг. Основные переменные: х 1 , х 2 , х 3 , х 4 ; неосновные переменные: х 5 , х 6 . Выразим основные переменные и линейную форму F через неосновные, начав это выражение из четвертого уравнения системы (4.6). В итоге получим

Так как в выражение линейной формы переменные х 5 и х 6 входят с отрицательным коэффициентами, то никакое увеличение F за счет этих переменных невозможно.

Отсутствие на каком-то шаге симплексного метода в выражении линейной формы F, максимум которой ищется, неосновных переменных с положительными коэффициентами является критерием оптимальности.

Следовательно, на 4 шаге критерий оптимальности достигнут и задача решена. Оптимальным служит решение (40; 20; 40; 0; 0; 0), при котором F max =140. Таким образом, для получения наибольшей прибыли, равной 140 ден. ед., из данных ресурсов необходимо получить 40 единиц продукции с сенокосов и 20 с пашни. При этом ресурсы II, III и IV видов окажется использованной полностью, а 40 ед. I вида останутся неизрасходованными.

Пример 4.2. Найти максимум функции F = х 1 + 2·х 2 при ограничениях

Вводим добавочные неотрицательные переменные х 3 , х 4 , х 5 , х 6 и сводим данную систему неравенств к эквивалентной ей системе уравнений

Введенные добавочные переменные принимаем за основные, так как в этом случае базисное решение системы легко находится. Тогда х 1 и х 2 - неосновные переменные.

1 шаг. Основные переменные: х 3 , х 4 , х 5 , х 6 ; неосновные перемен­ные; х 1 и х 2 . Выразив основные переменные через неосновные, получим

Следовательно, данному разбиению переменных на основные и неосновные соответствует базисное решение (0; 0; - 2; - 4; 2; 6), которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное. От этого базисного решения перейдем к улучшенному.

Чтобы решить, какую переменную следует перевести из неосновных в основные, рассмотрим любое из двух имеющихся уравнений последней системы с отрицательными свободными членами, например второе. Оно показывает, что в основные переменные можно перевести х 1 и х 2 , так как в этом уравнении они имеют положительные коэффициенты (следовательно, при их увеличении, что произойдет, если переведем любую из них в основные переменные, переменная х 4 увеличится).

Попробуем перевести в основные переменную х 1 . Чтобы установить, какую переменную следует перевести из основных в неосновные, найдем абсолютную величину наименьшего отношения свободных членов системы к коэффициентам при х 1 , имеем х 1 = min (∞; 4/1; 2/1; ∞) = 2. Оно получено из третьего уравнения, показывающего, что в неосновные нужно перевести переменную х 5 , которая в исходном базисном решении положительна.

Следовательно, полученное базисное решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому базисному решению улучшения не произойдет.

Если же перевести в основные переменную х 2 , то наименьшее отношение свободных членов к коэффициентам при х 2 составит х 2 - min (2/2; 4/1; ∞; 6/1) = 1. Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно, переводя х 2 в основные, а х 3 в неосновные переменные, мы получим базисное решение, в котором число отрицательных компонент на единицу меньше, чем в исходном. Поэтому остановимся на этой возможности: переводим х 2 в основные, а х 3 в неосновные переменные; тогда выделенным окажется первое уравнение.

2 шаг. Основные переменные: х 2 , х 4 , х 5 , х 6 ; неосновные переменные: х 1 и х 3 . Выразим новые основные переменные через новые неосновные, начиная это делать с выделенного на 1 шаге уравнения. В результате получим

Следовательно, имеем новое базисное решение (0; 1; 0; -3; 3; 5), которое также является недопустимым, а поэтому не оптимальным. Но в нем, как мы и предвидели, только одна переменная отрицательна (а именно х 4).

От полученного базисного решения необходимо перейти к другому. Рассмотрим уравнение с отрицательным свободным членом, т.е. второе уравнение. Оно показывает, что в основные переменные можно перевести х 1 и х 3 . Переведем в основные переменные х 1 . Найдем наименьшее из абсолютных величин отношений свободных членов системы к коэффициентам при х 1 ; имеем х 1 = min (∞; 3/1,5; 3/0,5; 5/0,5) = 2. Значит, в неосновные переменные нужно перевести х 4 . Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом базисном решении уже не окажется отрицательных компонент, т. е. оно является допустимым.

3 шаг. Основные переменные: х 1 , х 2 , х 5 , х 6 ; неосновные переменные: х 3 , х 4 . Выразив основные переменные через неосновные, получим

Новое базисное решение имеет вид (2; 2; 0; 0; 2; 4). Является ли оно оптимальным, можно установить, если выразить линейную форму через неосновные переменные рассматриваемого базисного решения. Сделав это, получим . Таким образом, к линейной форме обращаемся только тогда, когда базисное решение является допустимым. Так как мы ищем максимум линейной формы, то полученное базисное решение не оптимальное.

Переводим в число основных переменную х 4 имеющую больший положительный коэффициент.

Находим х 4 = min (∞; ∞; 2: (1/3); 4/(1/3)) = 6. Это наименьшее отношение получено из третьего уравнения системы, которое и выделяем. Оно показывает, что при х 4 =6 переменная х 5 = 0 и поэтому перейдет в число неосновных.

4 шаг. Основные переменные: х 1 , х 2 , х 4 , х 6 ;неосновные переменные: х 3 , х 5 . Выразив основные переменные через неосновные, получим

Линейная форма, выраженная через те же неосновные переменные, примет вид . Следовательно, базисное решение (6; 4; 0; 6; 0; 2), к которому мы перешли, не является оптимальным.

Увеличение линейной формы возможно при переходе к новому базисному решению, в котором переменная х 3 является основной. Находим х 3 = min {∞; ∞; со; 2/1} = 2. Это наименьшее отношение получено из четвертого уравнения системы и показывает, чго при х 3 = 2 переменная х 6 = 0 и переходит в число неосновных.

5 ш а г. Основные переменные: х 1 , х 2 , х 3 , х 4 неосновные переменные х 5 , х 6 .Выразив основные переменные через неосновные, получим

Линейная форма, выраженная через неосновные переменные нового базисного решения, имеет вид . Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно, базисное решение (8; 6; 2; 10, 0; 0) является оптимальным, а максимум линейной формы F max = 20.

4.5 Графическое решение задач

линейного программирования

Графический способ решения задач линейного программирования целесообразно использовать для:

Решения задач с двумя переменными, когда ограничения выражены неравенствами;

Решения задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.

Запишем задачу линейного программирования с двумя переменными:

целевая функция:

ограничения:

Каждое из неравенств (4.8) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми ; . В том случае, если система неравенств (4.8) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей - выпуклое, то областью допустимых ре­шений является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки равенств.

Областью допустимых решений системы неравенств (4.8) может быть:

Выпуклый многоугольник;

Выпуклая многоугольная неограниченная область;

Пустая область;

Отрезок;

Единственная точка.

Целевая функция (4.7) определяет на плоскости семейство параллельных прямых, каждой из которых соответствует определенное значение Z.

Вектор c координатами и , перпендикулярный этим прямым, указывает направление наискорейшего возрастания Z, а противоположный вектор - направление убывания Z.

Если в одной и той же системе координат изобразить область допустимых решений системы неравенств (4.8) и семейство параллельных прямых (4.7), то задача определения максимума функции Z сведется к нахождению в допустимой области точки, через которую проходит прямая из семейства Z = const, и которая соответствует наибольшему значению параметра Z.

Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение.

Для определения данной вершины построим линию уровня проходящую через начало координат и перпендикулярную вектору , и будем передвигать ее в направлении вектора до тех пор, пока она не коснется последней крайней (угловой) точки многоугольника решений. Координаты указанной точки и определяют оптимальный план данной задачи.

Рисунок 4.1 - Оптимум функции Z достижим в точке А

Рисунок 4.2 - Оптимум функции Z достигается в любой точке [АВ]

Заканчивая рассмотрение геометрической интерпретации задачи (4.7) - (4.8), отметим, что при нахождении ее решения могут встретиться случаи, изображенные на рис. 4.1 - 4.4. Рисунок 4.1 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке А. Из рисунка 4.2 видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ.

Рисунок 4.3 - Оптимум функции Z недостижим

Рисунок 4.4 - Область допустимых решений - пустая область

На рисунке 4.3 изображен случай, когда максимум недостижим, а на рисунке 4.4 - случай, когда система ограничений задачи несовместна. Отметим, что нахождение минимального значения Z при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня Z передвигается не в направлении вектора , а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.

Для практического решения задачи линейного программирования (4.7) - (4.8) на основе ее геометрической интерпретации необходимо следующее.

1.Построить прямые, уравнения которых получаются в результате замены в ограничениях (4,4) знаков неравенств на знаки равенств.

2.Найти полуплоскости, определяемые каждым из ограничений задачи.

3.Определить многоугольник решений.

4.Построить вектор .

5.Построить прямую , проходящую через начало координат и перпендикулярную вектору .

6.Передвигать прямую в направлении вектора , в результате чего либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность функции сверху на множестве планов.

7.Определить координаты точки максимума функции и вычислить значение целевой функции в этой точке.

Пример 4.3. Предприятие изготавливает два вида продукции П и Р, которая поступает в оптовую продажу. Для производства продукции используют два вида сырья А и Б. Максимально возможные запасы сырья в сутки составят 9 и 13 единиц соответственно. Расход сырья вида А на производство продукции П и Р составят 2 и 3 единицы соответственно, вида Б 3 и 2 единицы. Опыт работы показал, что суточный спрос на продукцию П никогда не превышает спроса на продукцию Р более чем на 1 единицу. Кроме того известно, что спрос на продукцию Р никогда не превышает 2 единицы в сутки. Оптовые цены единицы продукции равны 3 единицы для П, и 4 единицы для Р. Какое количество продукции каждого вида должно произвести предприятие, чтобы доход от реализации был максимальным. Решить задачу геометрическим способом.

Решение. Построим многоугольник решений (рис. 7.5). Для этого в системе координат X 1 OX 2 на плоскости изобразим граничные прямые:

Взяв какую-либо точку, например начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рис. 7.5 показаны стрелками. Областью решений является многоугольник OABCD.

Для построения прямой строим вектор-градиент и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z= 0 перемещаем параллельно самой себе в направлении вектора . Из рисунок 4.5 следует, что по отношению к многоугольнику решений опорной эта прямая становится в точке С, где функция принимает максимальное значение. Точка С лежит на пересечении прямых L 1 и Z 3 . Для определения ее координат решим систему уравнений:

Оптимальный план задачи = 2,4; =1,4. Подставляя значения и в линейную функцию, получим:

3 2,4 + 4 1,4 = 12,8.

Полученное решение означает, что объем производства продукции П должен быть равен 2,4 ед., а продукции Р - 1,4 ед. Доход, получаемый в этом случае, составит: Z = 12,8 д. е.

Рисунок 4.5 - Решение задачи линейного программирования геометрическим способом

5. ДВОЙСТВЕННЫЕ ЗАДАЧИ

Составление двойственной задачи. Рассмотрим две задачи линейного программирования:

Максимизировать функцию

при ограничениях

Минимизировать функцию

при ограничениях

Эти задачи обладают следующими свойствами:

1. В одной задаче ищется максимум линейной формы, а в другой – минимум.

2°. Коэффициенты при переменных в линейной форме одной задачи являются свободными членами системы ограничений другой задачи, наоборот, свободные члены системы ограничений одной задачи – коэффициентами при переменных в линейной форме другой задачи.

3°. В каждой задаче система ограничений задается в виде неравенств, причем все они одного смысла, а именно: при нахождении максимума линейной формы эти неравенства имеют вид, а при нахожде­нии минимума – вид

4°. Коэффициенты при переменных в системах ограничений описываются матрицами

которые являются транспонированными относительно друг друга.

5°. Число неравенств в системе ограничений одной задачи совпадает с числом переменных другой задачи.

6 е. Условия неотрицательности переменных сохраняются в обеих задачах.

Две задачи линейного программирования, удовлетворяющие указанным выше условиям, называются симметричными взаимно двойственными задачами. Мы будем изучать только симметричные двойственные задачи, а поэтому будем называть их короче – двойственными задачами.

Таким образом, каждой задаче линейного программирования можно поставить в соответствие двойственную ей задачу. Первоначальную задачу будем называть исходной (или прямой). Прямая и двойственная ей задача, взятые вместе, образуют пару взаимно двойственных задач, причем любую из них можно рассматривать как исходную, тогда другая окажется двойственной ей.

Из сказанного вытекают следующие правила составления задачи, двойственной по отношению к исходной:

1. Приводят все неравенства системы ограничений исходной задачи к неравенствам одного смысла: если в исходной задаче ищется максимум линейной формы – к виду ≤, если же минимум – к виду ≥. Для этого неравенства, в которых это требование не выполняется, умножают на - 1.

2. Выписывают матрицу А коэффициентов при переменных исходной задачи, полученных после преобразования п. 1, и составляют матрицу А", транспонированную относительно матрицы А.

3. Составляют систему ограничений двойственной задачи, взяв в качестве коэффициентов при переменных элементы матрицы А", а в качестве свободных членов – коэффициенты при переменных в линейной форме исходной задачи, и записывают неравенства противоположного смысла по сравнению с неравенствами, полученными в п. 1.

4. Составляют линейную форму двойственной задачи, приняв за коэффициенты при переменных свободные члены системы ограничений исходной задачи, полученные в п. 1.

5. Указывают, что необходимо найти при решении двойственной задачи, а именно: минимум линейной формы, если в исходной задаче ищется максимум, и максимум, если в исходной задаче ищется минимум.

6. Записывают условие неотрицательности переменных двойственной задачи.

Пример 5.1. Составить задачу, двойственную следующей: найти максимум функции при ограничениях

Третье неравенство системы (*) не удовлетворяет п. 1 правил составления двойственной задачи. Поэтому умножим его на –1:

Для облегчения составления двойственной задачи лучше пользоваться рас­ширенной матрицей В, в которую наряду с коэффициентами при переменных системы ограничений исходной задачи запишем свободные члены и коэффициенты при переменных в линейной форме, выделив для этой цели дополнительные столбец и строку. Матрицу В транспонируем и, используя транспонированную матрицу В / , составляем задачу двойственную данной.

Двойственная задача сводится к нахождению минимума функции при ограничениях

Основные теоремы двойственности

Теория двойственности в линейном программировании строится на следующих основных теоремах.

Теорема 1. Если одна из задач линейного программирования имеет конечный оптимум, то и двойственная к ней также имеет конечный оптимум, причем оптимальные значения линейных форм обеих задач совпадают, т. е. F max = Z min или F min = Z max . Если же линейная форма одной из двойственных задач не ограничена, то условия другой задачи противоречивы.

Прежде чем сформулировать следующую теорему, установим соответствия между переменными в исходной и двойственной задачах.

При решении симплексным методом исходной задачи для сведения системы неравенств к эквивалентной ей системе уравнений нужно ввести т добавочных неотрицательных переменных (по числу неравенств в системе ограничений) где i = 1, 2,…,т означает номер неравенства, в которое была введена добавочная переменная .

Система ограничений двойственной задачи состоит из п неравенств, содержащих т переменных. Если решать эту задачу симплексным ме­тодом, то следует ввести п добавочных неотрицательных переменных где j = 1, 2,…,т означает номер неравенства системы ограничений двойственной задачи, в которое была введена добавочная переменная .

Установим следующее соответствие между переменными в исход­ной и двойственной задачах:

Иными словами, каждой первоначальной переменной исходной
задачи x j (j = 1,2 ,…, п) ставится в соответствие добавочная переменная , введенная в j - e неравенство двойственной задачи, а каждой добавочной переменной исходной задачи (i = 1,2,…, т), введенной в i - e неравенство исходной задачи, – первоначальная переменная двойственной задачи.

Теорема 2. Компоненты оптимального решения одной из задач (прямой или двойственной) равны абсолютным величинам коэффициентов при соответствующих переменных в выражении линейной формы другой задачи (двойственной или прямой) при достижении ею оптимума и при условии, что полученное оптимальное решение не является вырожденным.

Из теорем 1 и 2 следует, что если решить одну из взаимно двойственных задач, т. е. найти ее оптимальное решение и оптимум линейной формы, то можно записать оптимальное решение и оптимум линейной формы другой задачи.

Пример 5.2. Решить симплексным методом прямую и двойственную задачи, приведенные в предыдущем примере.

Решение прямой задачи. Сведем систему ограничений неравенств (см. с. 268) к системе уравнений, введя неотрицательные добавочные переменные:

Добавочные переменные х 3 , x 4 , х 5 , x 6 примем за основные на I шаге реше­ния.

1 шаг. Основные переменные: х 3 , x 4 , х 5 , x 6 ; неосновные переменные: х 1 , х 2 . Выразим основные переменные через неосновные (линейную форму на этом шаге решения не рассматриваем, так как соответствующее базисное решение не является допустимым):

Для получения допустимого базисного решения переменную переведем в основные. Находим = min {2/1; ∞; 1/1; 5/1} = 1. При этом переменная х 5 переходит в неосновные.

2 шаг. Основные переменные: х 1 , х 3 , х 4 , х 6 неосновные переменные; х 2 , х 5 . Выразим основные переменные и линейную форму через неосновные:

Переведем в основные переменную х 5 . Полагая х 5 =min {∞; 1/1; ∞; 4/1} = 1, заключаем, что переменную х 3 нужно перевести в неосновные.

3 шаг. Основные переменные: х 1 , х 4 , х 5 , х 6 , неосновные переменные х 3 ,х 2 . Имеем

Переменную x 2 переводим в основные. Находим х 2 = min {∞; ∞;∞; 1/1}=1. Тогда переменная х 6 переходит в неосновные.

4 ш а г. Основные переменные:: х 1 , х 2 , х 4 , х 5 , ; неосновные переменные: х 2 , х 6 . Имеем

Критерий оптимальности выполнен. Оптимальное решение имеет вид (4; 1; 0; 5; 4; 0); при этом решении F max = 13.

Продолжение примера 5.1. Систему ограничений двойственной задачи сводим к системе уравнений:

Добавочные переменные y 5 y 6 примем за основные на 1 шаге решения.

1 шаг. Основные переменные: y 5 , y 6 ; неосновные переменные: y 1 , у 2 , у 3 , у 4 . Выразим основные переменные через неосновные:

Переведем в основные переменную у 4 . Находим у 4 = mm (3/1: 1/1 = 1. Переменная y 6 переходит в неосновные.

2 шаг. Основные переменные: у 4 , y 5 неосновные переменные: y 1 , у 2 , у 3 , у 6 . Имеем

Переменную y 1 переведем в основные. Так как y 1 = min (∞; 2/3) = 2/3, то переменная y 5 переходит в неосновные.

3 шаг. Основные переменные y 1 , у 4 , неосновные переменные: у 2 , у 3 , y 5 , у 6 . Так как соответствующее базисное решение задачи является допустимым, то выразим через неосновные переменные не только основные, но и линейную форму:

Критерий оптимальности (для случая минимизации линейной формы) вы­полнен. Оптимальное решение имеет вид (2/3; 0; 0; 7/3; 0; 0), при этом Z min = 13.

Решив двойственную задачу, убеждаемся в справедливости первой части теоремы 1: двойственная задача тоже имеет конечный оптимум, причем Z min = =F max = 13.

Убедимся, что справедливо также и утверждение теоремы 2. Для этого запи­шем переменные прямой и двойственной задачи, соблюдая их соответствие;

Линейную форму, полученную на последнем шаге решения двойственной задачи, выразим через все переменные этой задачи:

Рассматривая коэффициенты при переменных y j в этой линейной форме и учитывая их соответствие с коэффициентами при переменных x i , получим решение (4; 1; 0; 5; 4; 0), совпадающее с оптимальным решением прямой задачи.

Замечание. Решив прямую задачу, можно сразу получить решение двойственной задачи. Если выразить линейную форму F, полученную на 4 шаге решения прямой задачи, через все переменные этой задачи, то получим

На основании теоремы 2, учитывая соответствие между переменными в прямой и двойственной задачах и взяв абсолютную величину коэффициентов при переменных, найдем оптимальное решение двойственной задачи (2/3; 0; 0; 7/3; 0; 0). При этом Z min =F max = 13.

6 ТРАНСПОРТНАЯ ЗАДАЧА

Данному случаю соответствует взаимная противоречивость ограничений, входящих в задачу.

2) Допустимое множество - выпуклый ограниченный многогранник.

Допустимое множество - выпуклое неограниченное многогранное множество.

Два последних случая достаточно легко представить в двух- или трехмерном измерении. В пространстве большей размерности понятие многогранника (многогранного множества) вводится абстрактно как пересечение гиперплоскостей и гиперполуплоскостей, определяемых соответствующими линейными уравнениями и неравенствами, входящими в состав ограничений задачи. Характерным свойством многогранника является наличие в нем особых точек - вершин .

Возможные случаи оптимальных решений (планов) задачи линейного программирования.

1) Задача не имеет оптимальных решений .

Данный случай может возникнуть: либо тогда, когда допустимое множество решений пусто ("не из чего выбирать" оптимальный план),

либо когда допустимое множество представляет собой неограниченное многогранное множество, и целевая функция на нем неограниченно возрастает (если L  max) или неограниченно убывает (при L min).

2) Задача имеет единственное решение (единственный оптимальный план).

Это решение обязательно совпадает с одной из вершин допустимого множества.

3) Задача имеет бесконечное множество оптимальных решений, заданное некоторым линейным образованием - ребром, гранью, гипергранью и т.д. Среди точек этого линейного образования имеются и вершины допустимого множества.

Таким образом, основное утверждение теории линейного программирования, в конечном итоге определяющее специфические способы его решения, можно сформулировать следующим образом:

Если задача линейного программирования имеет хотя бы один оптимальный план, то его следует искать среди вершин допустимого множества решений.

В следующем параграфе рассмотренные общие положения будут проиллюстрированы на примере задачи линейного программирования с двумя переменными.

1. Графоаналитический способ решения задач линейного программирования

Графоаналитический (графический) способ решения задач линейного программирования обычно используется для решения задач с двумя переменными, когда ограничения выражены неравенствами, а также задач, которые могут быть сведены к таким задачам.

Пусть задача линейного программирования имеет вид:

(1.7)

где с 1 , с 2 , а i 1 , а i 2 , b i - заданные действительные числа; знаки в неравенствах произвольны; целевая функция либо максимизируется, либо минимизируется.

Каждое из неравенств (1.7) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми
;i =1,…,m . В том случае, если система неравенств (1.7) совместна, допустимая область решений задачи есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых значений является выпуклое множество, которое называютмногоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки равенств.

Множеством допустимых решений для данной частной задачи может быть:

пустая область;

выпуклый многоугольник, включая вырожденные случаи - отрезок и единственную точку;

выпуклая многоугольная неограниченная область, включая вырожденные случаи - луч и прямую.

Практическая реализация решения задачи линейного программирования (1.6) – (1.7) на основе ее геометрической интерпретации включает следующие этапы:

1. Построить прямые, уравнения которых получаются в результате замены в ограничениях (1.7) знаков неравенств на знаки равенств.

2. Найти полуплоскости, определяемые каждым из ограничений.

Соответствующая полуплоскость может быть найдена подстановкой в неравенство координат какой-нибудь «простой» точки - (0,0), (0,1) или (1,0). Главное - чтобы эта точка не принадлежала границе полуплоскости. Если после подстановки неравенство окажется справедливым, то выбирается та полуплоскость, где содержится эта точка. Если неравенство не справедлива, то выбирается альтернативная полуплоскость.

3. Определить многоугольник решений, как пересечение найденных полуплоскостей.

4. Построить градиент целевой функции, т.е. вектор
, координатами которого служат коэффициенты целевой функцииL .

Этот вектор определяет направление наискорейшего возрастания целевой функции.

5. Построить ряд линий уровня целевой функцииL , т.е. прямых перпендикулярных градиентуL . При этом построение линий уровня следует вести в направлении градиента, если решается задача на максимум, и в противоположном направлении (в направлении «антиградиента»), если решается задача на минимум. В результате отмечается точка (точки), в которой линии уровня в последний раз касаются допустимого множества.

Если допустимое множество неограниченно, то точки последнего касания может и не быть. Линии уровня уходят в бесконечность, соответственно значение
или
, и задача не имеет оптимальных планов.

Определить координаты отмеченной точки аналитически, решая соответствующую систему линейных уравнений. Затем вычислить значение целевой функции в этой точке. Тем самым, определяется оптимальный план и оптимальное значение целевой функции задачи.

Заканчивая рассмотрение геометрической интерпретации задачи (1.6) – (1.7), отметим, что при нахождении ее решения могут встретиться случаи, изображенные на рис. 1.1 – 1.3. Рис. 1.1 характеризует такой случай, когда целевая функция принимает оптимальное значение в единственной точке А, одной из вершин допустимого множества. На рис. 1.2 оптимальное значение целевая функция принимает в любой точке отрезка АВ. На рис. 1.3 изображен случай, когда оптимальное значение целевой функции недостижимо.

Рис. 1.1. Оптимум функции L достижим в точке А

Рис. 1.2. Оптимум функцииL достигается в любой точке отрезка АB

Рис. 1.3. Оптимум функции L недостижим